Tight-Binding Approximation

In solid-state physics, a tight-binding approximation model is an approach to the calculation of electronic band structure using an approximate set of wavefunction based superposition of wavefunction for isolated atoms. here is the description about the Tight-Binding Approximation

If one solves the radial part of the Schrodinger equation for the hydrogen atom, one obtains the radial part of the eigenfunction for the 1s state as X = e-r/r0 • In the one-dimensional sketch, the eigenfunction decreases exponentially with r the nucleus from increases.

As two H atoms approach each other, the atomic wavefunction overlap. this overlapping of the wavefunction produces two new wavefunctions with different energies and hence different quantum numbers,

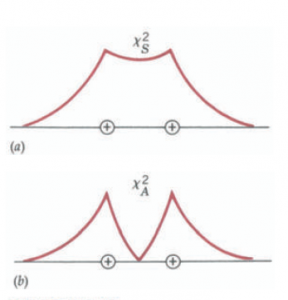
the two eigenfunctions can overlap either in phase forming symmetric eigenfunction XS = a (XB + Xc)

Photo

or in out of phase forming an antisymmetric eigenfunction XS = a (XB – Xc)

Photo

The figure given below shows that the probability function X2 is in the large region between two nuclei so the electron spends more time between both nuclei.in the region between the two protons is greater than on either side of the protons. In this region, it is under the attractive influence of both protons at once. The binding energy of the electron resulting from the presence of the two protons will be more negative than if it was only under the influence of one of them. Thus, when two atoms are brought together, two separate energy levels are formed from each level of the isolated atom. The physical reason for this effect is the differing ways that the electrons interact with the ions in the symmetric and antisymmetric states.

If we start with six individual Is states and consider all the possible ways of adding the six individual Is states, we get six types of combinations having different energies . In the first level, the six individual eigenfunctions all add symmetrically,

Xfirst level = X1+ X2 + X3 + X4 + X5 + X6

there are five places along the lattice where the electron will be under the attractive (binding) influence of two nuclei. In the second level, the X’s from the first three atoms add symmetrically among themselves and so do the last three, but the resulting X from the first three adds antisymmetrically with the resulting X from the last three:

X second level = (X1+X2 + X3) – (x4 + X5 + X6)

there are only four places along the lattice where the electron will be under the simultaneous influence of two nuclei that gives the extra negative contribution to the energy. The energy of an electron in this level will be higher than that of an electron in the first level.

There are more combination that can be obtained by permutation of these six X’s but other combination will be degenerate with one of the preceding as shown in the examples above

when we extend this analysis to a lattice of N atoms, the individual identical states of the atoms will give rise to N different energy states. However, regardless of the number, the two extremes will look like the first and sixth level of our example. It should also be apparent that the energy difference between the two extremes and, therefore the width of the band, should not depend appreciably on N. Increasing N increases the number of sites where the extra contribution to the el1ergy can take place. But it simultaneously decreases the amount of time that the electron spends in any one site, making the total time in all such sites constant. What affects the width of the band is how close any two atoms are to each other. The closer, the greater the overlap of the wavefunctions and therefore the larger X2 will be between the two nuclei for symmetric states, with the consequence of stronger binding.

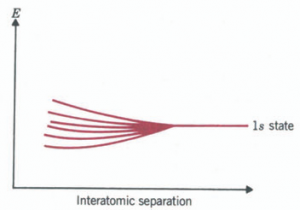
We thus have shown that when one brings a large number N of atoms together to form a solid, the individual atomic energy levels of the atom break up into a quasicontinuous energy band. Within the band, there are N distinct but very close energy levels.

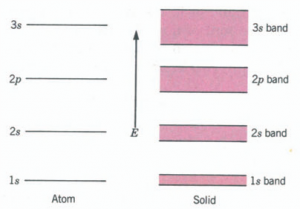
When the analysis is extended to multielectron atoms where we have electrons in other states, one finds that each of the individual atomic states breaks up into similar bands of quasi-continuous states. Thus, if we consider sodium (Na) with an electronic configuration Is2 2s2 2p6 3s1, we may expect the band structure illustrated schematically. Notice that the bandwidth for the low-lying levels is smaller than for the higher energy ones. The reason is that electrons in the lower levels are electrons in the inner subshells of the atoms; these electrons are not influenced much by the presence of other atoms because their wave functions do not overlap significantly with those of the electrons of other atoms. Therefore, they give rise to narrower bands.