Effective Mass

When an electric field ‘if; acts on a free electron, it exerts a force e’ if; that, from Newton’s law, will produce an acceleration inversely proportional to its mass, a = eε/m. What happens when the electron to be accelerated is not free but happens to be in a crystal under the influence of the potential of the lattice ions? The answer is that it will still accelerate according to Newton’s law; however, the electron responds as if it had some effective mass, which is different from its true mass. As we will show, this is because ‘if; is not the only electric field acting on the electron inside the crystal. We will introduce this concept by using a semi-classical picture: an argument that is half classical and half quantum mechanical. The quantum mechanical part lies in the fact that the motion of an electron is governed by a wave, and that the velocity of the electron is equal to the group velocity Vgroup of the wave, that is, the velocity of the envelope, of the wave packet. In our treatment of matter waves and wave packets, we saw that the group velocity is given by

vgroup = dE/dp

where E is the energy of the particle and p is its momentum. In the case of a free particle, we can readily show that the group velocity is equal to the particle velocity. For a free particle, the energy

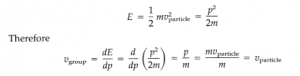
Although we have shown that Vgroup = Vparticle for the free particle case only, it can be shown that the relation holds even when the particle is not free, such

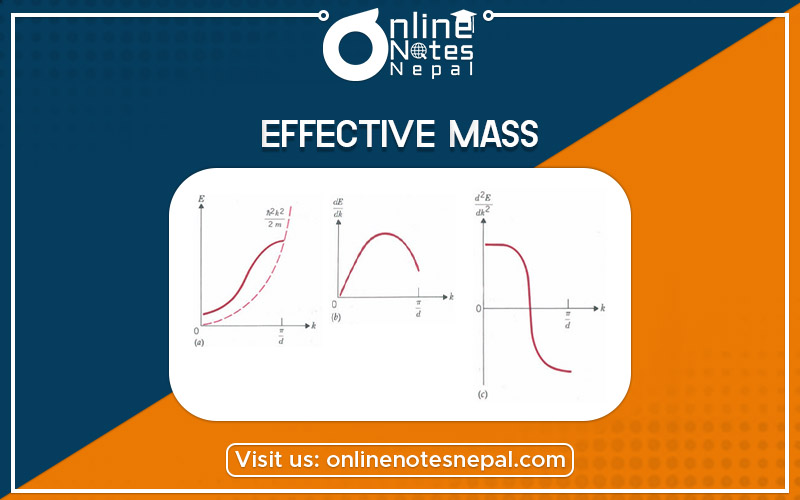
When the electron is free, the effective mass is the true mass, as it should be. However, when the electron is in a crystal, m* is different from m because the energy is not proportional to P, as we saw in the Kronig-Penney model. The physical reason is the following. The electron in the crystal moves under the influence of internal forces exerted by the electric fields of the ions of the lattice and the external force resulting from the externally applied electric field.I f we choose to use Eq. 24.8 to describe the motion of the electrons, we describe the motion in terms of the external force alone. However, the effect ofthe internal forces is hidden in m*. Let us recall the results that we obtained from the Kronig-Penney model concerning the relation between E and k (Fig. 24-10). The relation for the first allowed band is represented by the solid line in Fig. 24-30a.

Picture

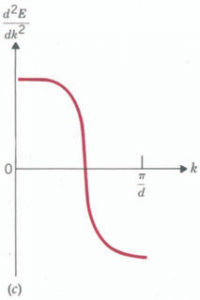
For small k’s both curves, the free electron one (the dashed line) and the one obtained from the model, are quite similar. Both the first and the second derivatives are almost the same; therefore, m is about equal to m*. Notice, however, that in the Kronig-Penney curve the first derivative (the slope) first increases for small values of k and then decreases as k approaches n/d. We illustrate a qualitative plot of the slope dEldk versus k in Fig. 24-30b. We may also draw a qualitative illustration of d2EldF from Fig. 24.30b.

Picture

Its appearance is that of Fig. 24-30c.The reciprocal of d2Eldk2 is proportional to the effective mass, from Eq. 24.9. These reciprocal curves are shown in Fig. 24-30d. We see that for small values of k the effective mass m* is essentially equal to the mass of a free electron m. As dEldk approaches the maximum, d2EldF begins to decrease and m*increases. When dEldk reaches the maximum, d2EldF = 0 and m* becomes infinite. Subsequently, d2EldF becomes negative and m* is negative. We may draw the following conclusions about the effective mass m* of an electron moving in a periodic lattice (see Fig. 24-30d).

1. m* is not always equal to m.
2. m* can be greater than m and, in fact, infinite.
3. m* can be less than m or even negative.

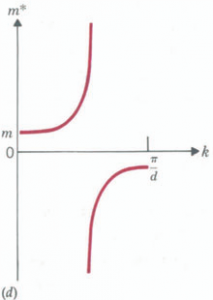
At the bottom of a band where k = 0, there is practically no reflection because the Bragg condition is far from being satisfied. The lattice ions will have little effect on the electron when it is accelerated by the external field. Higher-up in the band, k will get closer to the critical value T/d, and reflection starts to become appreciable. In this region, as the external field ~ accelerates the electron, the momentum increases and gets closer to the critical value. The external field increases the forward momentum, but at the same time enhances reflection, and the reflection corresponds to reversing the sign of the momentum.

At the point where lm* = 0 (that is, m* = (0), the gain in the forward momentum resulting from the applied ~ is exactly compensated by the resulting enhancement in reflection by the lattice ions. The net change in the forward momentum is zero. Thus the overall response of the electron to the field ~ is as if it had an infinite mass; that is, it cannot be accelerated.

At the top of the band, even closer to the critical value for total reflection, the second effect (enhanced reflection) is more important than the direct action of the applied field. The net result is that the electron responds with a change in momentum that is in the opposite direction to what the free electron would have acquired: the electron responds as if it had a negative mass.