Bloch’s Theorem

There are two theories regarding the band theory of solids they are Bloch’s Theorem and Kronig Penny Model Before we proceed to study the motion of an electron in a periodic potential, we should mention a general property of the wave functions in such a periodic potential.

For a free electron with Ep = constant, the space part of the wave function Ψ (x, t), called the Eigenfunction x(x), is written as

x(x)= e+-ikx

If the spacing of the ions in the x-direction in a solid is d, then the potential energy of an electron at a point x distance from the origin is equal to the potential energy at a point x + d from the origin. This potential energy is equal in turn to that at point x + 2d from the origin, and so on. Therefore, we can generalize and take any point x in the lattice and state that the potential energy at that point is equal to the potential energy at point x + d or, stated mathematically,

Ep(x) = Ep (x + d).

This is known as a periodic potential. There is a theorem by Bloch which states that for a particle moving in a periodic potential, the Eigenfunctions x(x) is of the form

X(x) = Uk(x) e+-ikx

where

Uk (X) = Uk (X + d)

These Eigenfunctions are plane waves modulated by a function Uk(X), where Uk(X) has the same periodicity as the potential energy. Because the potential energy Ep(x) = Ep (x + d), one expects that the probability of finding a particle at a given x is the same as that of finding it at x + d. This is guaranteed by the periodicity of Uk and can be seen in the following expression for the probability density.

Therefore, when

x*(x) x(x) = uk*(x)e-ikx uk(x) eikx

= uk*(x)  uk(x)

then

x*(X) X(x) = x*(x + d) X (x + d)

The specific form of the function Uk(X) will depend on the form of the function Ep(x) . We will now consider an idealized, one-dimensional periodic potential.

Kronig Penny Model

According to the quantum free electron theory of metals, a conduction electron in a metal experiences constant (or zero) potential and free to move inside the crystal but will not come out of the metal because an infinite potential exists at the surface. This theory successfully explains electrical conductivity, specific heat, thermionic emission, and Paramagnetism. This theory fails to explain many other physical properties, for example: (i) it fails to explain the difference between conductors, insulators and semiconductors, (ii) positive Hall coefficient of metals, and (iii) lower conductivity of divalent metals than monovalent metals.

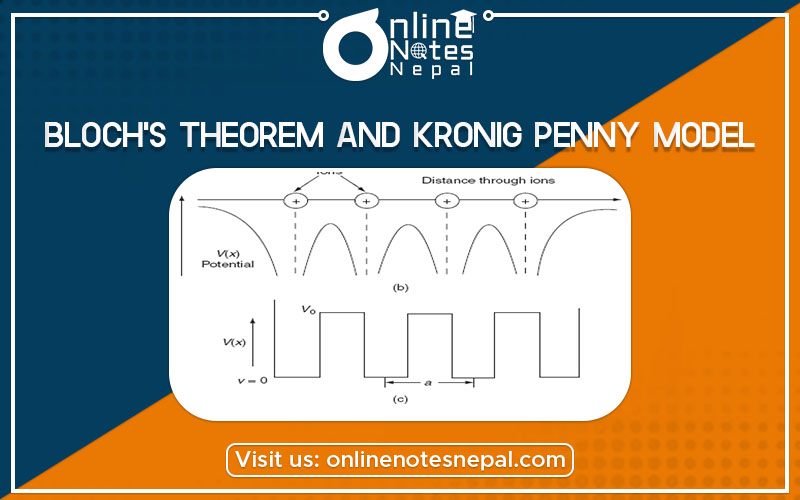
To overcome the above problems, the periodic potentials due to the positive ions in metal have been considered. shown in Fig. (a), if an electron moves through these ions, it experiences varying potentials. The potential of an electron at the positive ion site is zero and is maximum in between two ions. The potential experienced by an electron, when it passes along a line through the positive ions is as shown in Fig. (b).

picture

It is not easy to solve Schrödinger’s equation with these potentials. So, Kronig and Penney approximated these potentials inside the crystal to the shape of rectangular steps as shown in Fig. (c). This model is called the Kronig-Penney model of potentials.

Picture

The energies of electrons can be known by solving Schrödinger’s wave equation in such a lattice. The Schrödinger time-independent wave equation for the motion of an electron along X-direction is given by:

Equation ……………(1)

The energies and wave functions of electrons associated with this model can be calculated by solving time-independent one-dimensional Schrödinger’s wave equations for the two regions I and II as shown in Fig

The Schrödinger’s equations are:

Equation for 0

Equationfor -b

We define two real quantities (say) α and β such that:

Equation

Hence, Equations (1) and (2) becomes:

Equationfor 0

Equationfor -b

According to Bloch’s theorem, the wave function solution of the Schrödinger equation when the potential is periodic and to make sure the function u(x) is also continuous and smooth, can be written as:

Equation

Where u(x) is a periodic function which satisfies u (x + a) = u(x).

Using Bloch theorem and all the boundary conditions for the continuity of the wave function the solution of Schrodinger wave equation obtained as

Equation

where

Equation

This equation 5.59 shows the relation between the energy (through α) and the wave-vector, k, and as you can see, since the left-hand side of the equation can only range from −1 to 1 then there are some limits on the values that α (and thus, the energy) can take, that is, at some ranges of values of the energy, there is no solution according to these equations, and thus, the system will not have those energies: energy gaps. These are the so-called band-gaps, which can be shown to exist in any shape of periodic potential (not just delta or square barriers). This has been plotted in Fig.

Picture

The permissible limit of the term

Equation

lies between +1 to -1. By varying αa, a wave mechanical nature could be plotted as shown in Fig, the shaded portion of the wave shows the bands of allowed energy with the forbidden region as an unshaded portion

If you liked our content Bloch’s Theorem and Kronig Penny Model then please don’t forget to check our other topics, Metallic Bond and Molecular Bond