Published by: sadikshya
Published date: 21 Jun 2021
PICTURE
Fig. The energy in Simple Harmonic Motion
The total energy of an oscillating particle in simple harmonic motion is the sum of its KE and PE if a conservative force acts on it.
The velocity of a particle executing SHM at a position where its displacement is y from its mean position is v = ω√a2 – y2
The kinetic energy of the particle of mass m is,
PICTURE
From the definition of SHM F = –ky the work done by the force during the small displacement dy is dW = −F.dy = −(−ky) dy = ky dy
∴ Total work done for the displacement y is,
PICTURE
This work done is stored in the body as potential energy.
PICTURE
Thus we find that the total energy of a particle executing simple harmonic motion is ½ mω2a2.
PICTURE
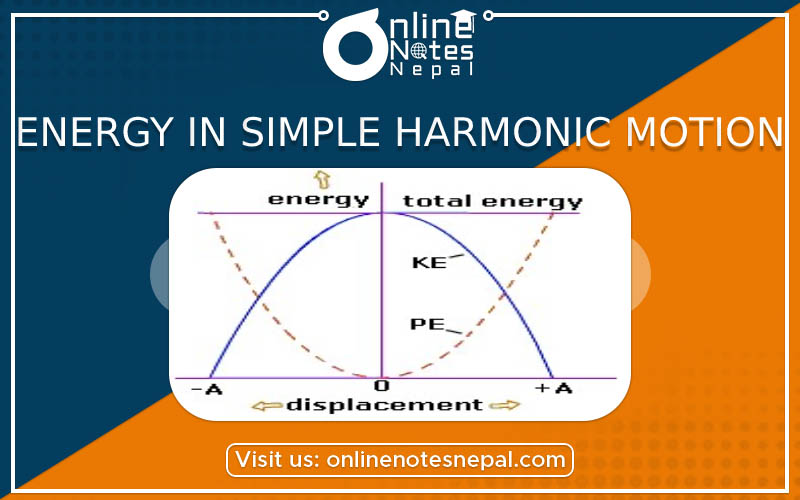
Fig. Energy Displacement Diagram
(i) When the particle is at the mean position y = 0, from Eqn (1) it is known that kinetic energy is maximum and from Eqn. (2) it is known that potential energy is zero. Hence the total energy is wholly kinetic.
PICTURE
(ii) When the particle is at the extreme position y = +a, from equation (1), it is known that kinetic energy is zero and from Eqn. (2) it is known that Potential energy is maximum. Hence the total energy is wholly potential.
PICTURE
(iii) When y = a/2,
PICTURE
If the displacement is half of the amplitude, K = ¾ E and U = ¼ E. K and U are in the ratio 3: 1.
PICTURE
At any other position, the energy is partly kinetic and partly potential.
This shows that the particle executing SHM obeys the law of conservation of energy.