Classical Free Electron Model

Assumptions of Classical Free Electron Model are as follows;

• In a metallic conductor, ions are in array form with valance electron free to move. Hence, conduction takes place due to the movement of free electrons.
• The repulsion between electrons is negligible.
• In the absence of electric field, electrons move in random direction with velocity ½ mv2 = 3/2 KT,

Where, k = Boltzmann Constant and T = Absolute Temperature.

• In the presence of an electric field, the electron moves with an average velocity called drift velocity in the opposite direction of the electric field.

It is used to derive Ohm’s law as follows;

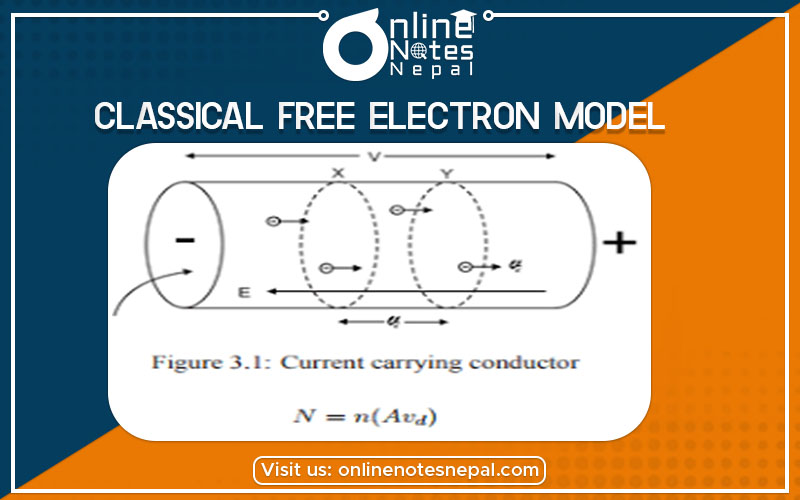
Let us consider a cylindrical metallic conductor having length ‘l’ and cross-sectional area ‘A’. Again, n is the number of free electrons per unit volume. If ‘v’ is the velocity of an electron moving with distance ‘x’ in time ‘t’, then,

Distance(x) = vd × t

Total number of electron(N) = n × vol.

Or, N = n × A × distance

= n × A × vd × t ……(i)

Now, current is rate of flow of charge,

I = Q/t

i.e. I = Ne/t    ……(ii)

From equation (i) and (ii)

I = (n × A × vd × t × e)/t

i.e. I = vdenA …..(iii)

Now, Current Density (J) = I/A = (vdenA)/A

Therefore, J = vden ……(iv)

 

If Fe is the electric force then,

Fe= Ee

Or, ma = eE   (F=ma)

Or, a = eE/m

Or, dv/dt = eE/m

Or, dv = dt. eE/m

Integrating on both sides we get,

Vd = eEτ/m  …….(v)

Where τ = Relaxation Time

From (iv) and (v)

J = vden

= (eEτ × en)/m

= (ne2τ × E)/m

Hence,

J = σE

[i.e. (ne2τ)/m = σ = electrical conductivity]

Which is Ohm’s law.

Failures of classical free electron

1) Specific head:-

The molar specific heat of a gas at constant volume is cv= 2/2 RT but experimentally it was found that the specific heat of a metal by its conduction e was CV=10-4 RT which shows dependence on temperature which is contra vary to the theory.

2)The temperature-dependent electrical conductivity of a metal experimentally was found that

Expt𝜎 ∝⊥/𝑇
The theoretical was found that
Theort𝜎 ∝⊥/√𝑇

3)Dependence of electrical conductivity on electron concentration.

4) 𝜎 =ne2T/m

n—> electron concentration.
Cu 8.2×1028 e/m3
A1 18.06X1028 e/m3
A1 > CU—> classical theory
Cu̇ 𝜎 A1 experimentally