Matter waves 

Matter waves and Uncertainty Principle:

The spatial propagation of a particle can be represented by a simple sinusoidal function as,

Ψ(x,t) =  A sin(kx-ꙍt)     ……(1)

This particular wave has the following properties:

a. The amplitude A is same at all points in space.

b. It has a well-defined wavelength, λ = 2 π/k

c. It has a well-defined frequency, f = λ/2 π

d. It travels towards increasing values of x with a velocity v = f λ = ꙍ/k

Here the amplitude of the wave is the same for all values of x, the particle can be found with equal probability at any point in space, that is, the particle is completely unlocalized, ∆x = ꚙ.

However, a well-defined λ implies a well-defined momentum for the particle, that is, ∆Px = 0. Which is in agreement with uncertainty principle.

Here the velocity of the wave,

v = f λ = (E/h) * (h/P)

v = E/P

But, for a particle, E = ½ mv2, and P = mv

Therefore, wave velocity V = (½ mv2)/(mv) = ½ v

This shows that the velocity of wave is not as same as the velocity of particle that it guides.

To describe a particle that is partially localized, we need a wave with a different amplitude that looks like the wave packet. In this case, in a small region of space, there is a chance of finding a particle.

Picture

Fig: A wave packet

Mathematically, such a wave packet is obtained by mixing an infinitely large number of sinusoidal waves of the type described by equation(1). Each of these waves differs wavelength and frequency by an infinitesimally small amount. Thus, the amplitude becomes the function of the wavelength and frequency. Thus, we can express the wave packet as an integral with respect to k and w, because, f = (ꙍ/2 π and λ = 2 π/k).

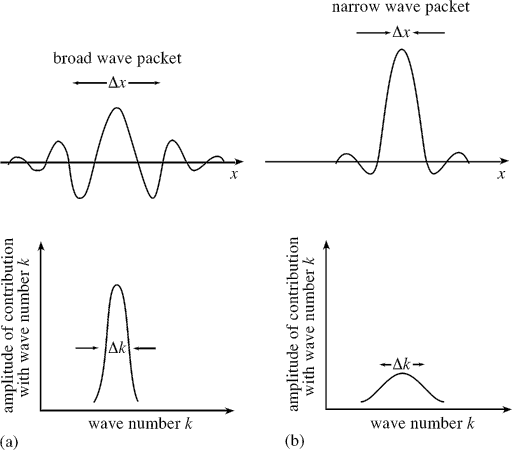
Fig(2): Wave packets obtained by mixing sinusoidal travelling waves of different wavelength and frequency

Mathematical treatment shows that when we mix various sinusoidal waves of slightly different wavelength and frequency, the spatial variation of Ψ at t = 0 look as shown in figure (2). The graph to the left shows the form of A, and the graph to the right shows the resulting wave packet Ψ.

From figure(2), it is seen that the greater the range of frequency, the narrower is the wide of resulting wave packet. To localize the particle, we must mix waves with a range of frequencies. In this case, the wave packet doesn’t have a well-defined wavelength, the particle associated with it will not have a well-defined momentum. This verifies the uncertainty principle.