Application of The Schrodinger Theory

Schrodinger developed a differential equation whose solutions yield the possible wave functions that can be associated with a particle in a given physical situation. This equation, known as the Schrodinger equation, tells us how the wave function changes as a result of the forces acting on the particle.

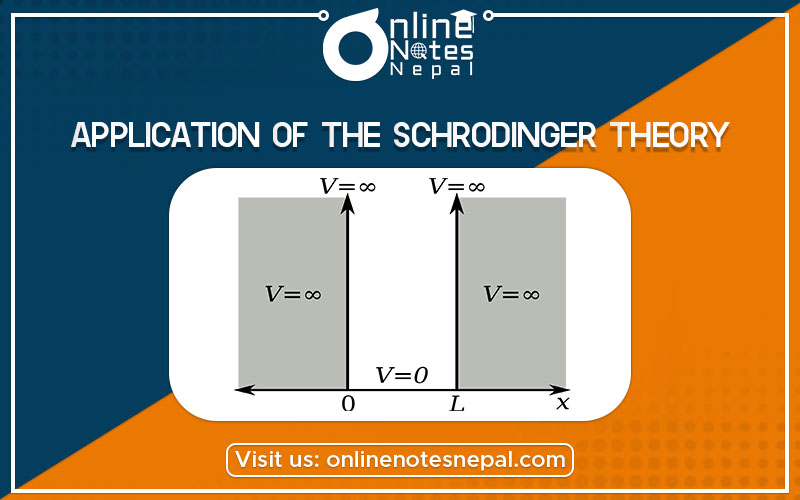
A Particle Inside An Infinite Potential Well

Picture

In order to know about the application of the Schrodinger theory, Let us consider a particle such as an electron confined inside a one-dimensional well of length with infinitely high walls. The potential of the particle V is zero inside the box but raises to infinity on the outside. i.e.

V= 0 for 0< x< L

V= ∞ for 0> x> L

The time independent Schrodinger wave equation is:

Equation

the trigonometric solution of eqn (1) is

Ψ(x) = A sinkx + B coskx __ (3)

{A and B are two arbitrary constant}

Now, applying boundary conditions we get:

at x= 0: B= 0

at x= L

A sinkL= 0

sinkL= sin nπ

k= nπ/L

k2= n2 π2 /L2 __ (4)

the discrete energy can be calculated by comparing Eqn (2) and (4)

Equation

The quantized value of energy for different levels can be calculated for free particles inside the box.

Now, Eqn (3) can be written as:

Ψ(x) = A sinkx + B coskx

Ψ(x) = A sin (nxπ/L)

using normalization condition we have,

Equation

Hence the Equation for a free particle in the well is:
Ψ(x) = √(2/L) sin (nxπ/L)

If you liked our content Application of The Schrodinger Theory then please don’t forget to check our other topics Schrodinger theory