Conductors Insulators and Semiconductors

The solids can be classified into Conductors Insulators and Semiconductors. To understand why some solids are good conductors, and some are not. We must keep in mind two facts.

1. For electrons to experience an acceleration in the presence of an electric field % and therefore to contribute to the current, they must be able to move into new, slightly higher energy states. This means that the states that are available for the electrons must be both empty and For example, if relatively few electrons reside in an otherwise empty band, a large number of unoccupied states are available into which the electrons can move; these electrons can acquire energy from the electric field and contribute to the current. On the other hand, if a band is full, then the electrons in that band cannot contribute to the current because they cannot move into slightly higher energy states. They therefore cannot be accelerated by the electric field.

1. There is a limit to the number of electrons that can be placed in a given band. We know that there are N different energy states in each band. If the band is an s band (one formed from atomics states) then, the orbital quantum number I = 0 and therefore ml = 0 and ms = ± 112. We can place two electrons in each of the N states without violating Pauli’s exclusion principle. In a p band I = 1, ml = 0, 1, -1 and for each value of ml, ms = ± In each of the N energy levels we can put six electrons. In general, because for a given I there are (21 + 1) values of ml and for each ml there are two values of ms , we have 2(21 + I)N openings available to the electrons in a given band; for example, in a d band, the number is 2(2 x 2 + I)N = 10 N.

Let us consider some hypothetical examples on the basis of these two facts. Consider a solid of N atoms with each atom having 11 electrons. Altogether there are 11N electrons. 2N electrons may be put in the Is band, 2N in the 2s band, 6N in the 2p band. There remain N electrons that may be placed in the next available band, the 3s. But the 3s band has room for 2N electrons, and therefore it will be only half full (see Figure).

photo

As a consequence, half the states in the 3s band (the unoccupied ones) are available to the N electrons in that band. Because there are available states, the N electrons in this band can be accelerated by an electric field and move into higher energy states. This solid would be an electrical conductor.

Note that because the N electrons in the 3s band obey the Pauli exclusion principle, they obey Fermi Dirac’s statistics; that is, at T = 0 K they all reside in the lowest energy levels of the band and the highest occupied level becomes the Fermi level. For T > 0, a few (as we saw in the previous chapter) can be above the Fermi level. The N electrons in the 3s band behave as predicted by the QMFE model with one minor modification that we will discuss later. We can see that the effect of the periodic potential on the motion of electrons in a solid with a partially filled band is unimportant, and that is the reason why the QMFE model was so successful in predicting the properties of conductors. This hypothetical solid is of course Na (2 = 11). The only difference between the hypothetical solid and the real Na is that in sodium metal the next band, the 3p, overlaps the 3s band. But all that this does is to provide additional empty energy levels for the N electrons in the 3s band. The same arguments used for Na apply to lithium (ls2 2S1), potassium (ls2 2S2 2p6 3s2 3p6 4s1), as well as to rubidium and cesium.

It should be noted that the highest energy band containing electrons is called the valence band. If, as in the case of sodium, this band is only partially filled, it is also called the conduction band because electrons in that band are responsible for conduction processes.

Next consider magnesium (2 = 12) with electronic configuration Is2 2S2 2p6 3s2. In a solid with N atoms, there are 12N electrons. Following the previous scheme, 2N electrons go into the Is band, 2N into the 2s, 6N into the 2p, and the remaining 2N into the 3s. All 12N electrons have been accounted for in the process. They have completely filled the 3s band. According to our previous argument, there are no empty energy states available for the electrons in the 3s band to move into; therefore, they cannot contribute to conduction. With no empty states through which charged particles may contribute to conduction, Mg should be an insulator. But it is not. The reason is that as in the case of Na, the 3p and 3s bands overlap (see Figure below).

photo

Because the 3p band has 6N empty states, the 2N electrons have available to them 2N + 6N states of which only 2N are occupied. Mg is therefore a conductor. Similar arguments apply to beryllium, calcium, zinc, and barium, all of which are in the same group in the periodic table.

Now consider carbon (ls2 2S2 2p2) in its diamond structure. As N atoms of C are brought together, they have 6N electrons. 2N fill the Is band, 2N fill the 2s band, and there are 2N electrons left to place in the next available band, the 2p, which has room for 6N electrons. The 2p band would be a partially filled band with plenty of empty states available (see Figure below).

photo

Diamond should, therefore, be a conductor. But it is not. It is an excellent insulator. As we mentioned before, the qualitative arguments elucidate the main features of the band structure. However, when dealing with a specific crystalline material, the arguments must become quantitative. When this is done, interesting features occur, such as band overlap. In the case of diamond, germanium, and silicon, and even more interesting feature is revealed.

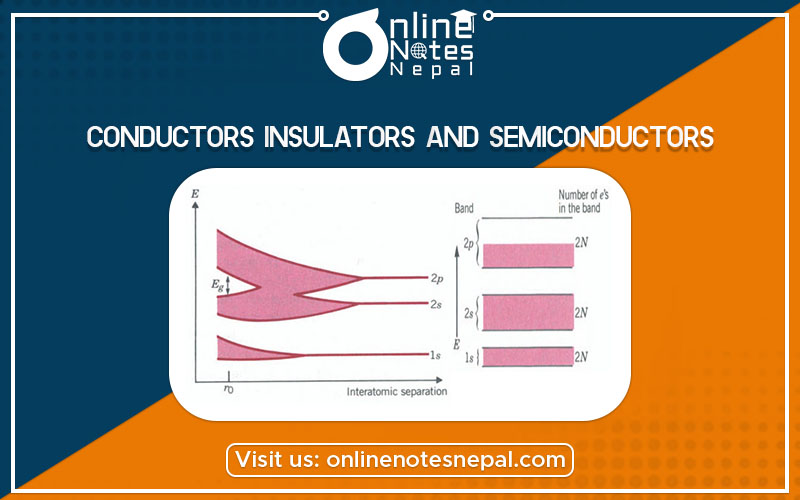
As the carbon atoms are brought together to form a diamond, the energy levels begin to split into bands starting with the outermost shell, n = 2 (2s and 2p levels) (Figure below).

photo

As the interatomic spacing decreases farther, the 2s and 2p bands begin to overlap and merge into a single ‘2s 2p’ band with 8N states available. As the separation decreases even farther, approaching the interatomic equilibrium spacing r0, the ‘2s 2p’ band splits again into two-hybrid bands separated by an energy gap Eg, which increases with decreasing separation. The value of Eg is about 6 eV for the equilibrium distance of r0 =b1.5 x 10- 10 m. However, each of these two bands now contains 4N states. The result: Of the total 6N electrons, 2N go into the Is band and the remaining 4N into the lower hybrid ‘2s 2p’ band and fill it. Thus, at T = 0 K the valence band (the lower ‘2s 2p’ band) is full (see figure below), and diamond is an insulator.

photo

Note that this is only true for the diamond structure of carbon, not for graphite. The bands of germanium (Ge) and silicon (Si) show a similar behavior. In the case of Si, the mixing and subsequent splitting occur between the 3s and 3p, whereas in the case of Ge it occurs between the 4s and the 4p. There is, however, an important quantitative difference between diamond and Si and Ge. The energy gap Eg between the filled valence band and the next empty band for Ge and Si is much smaller than for C: Eg (Ge) = 0.7 eV, Eg (Si) = 1.1 eV. At T = 0 K, pure C, Si, and Ge behave identically. They are perfect insulators because the valence band is filled. However, as T increases, some of the electrons in the valence band can be thermally excited across the energy gap into the next band, which now becomes the conduction band, and as a result electrical conduction can take place. How many electrons can be excited depends on how big Eg is and, of course, on T. The higher T, the greater the thermal energy, and therefore the greater the number of electrons that will be able to make the jump across the energy gap and, naturally, the greater the electrical conductivity. This is the reason why the conductivity of an insulator and of a semiconductor increases with T (as opposed to a metallic conductor). We will discuss this further in the next chapter. The number of electrons in the conduction band at a given temperature will depend on Eg, the magnitude of the energy gap between the valence and the conduction bands. The smaller Eg, the greater the probability that the electrons at the top of the valence band will jump into the conduction band.

Thus, at a given temperature, we expect that Si (Eg = 1 eV) will have more electrons in the conduction band and therefore, be a better conductor than diamond (Eg = 6 eV). In fact, as we will show in Chapter 25, the probability of transition across the energy gap is very sensitive to the magnitude of Eg • A doubling of Eg will reduce the number of conduction electrons by several orders of magnitude (powers of 10). It is the magnitude of Eg that determines whether a solid is an insulator (diamond) or a semiconductor (Si, Ge) at ambient temperatures.

If you liked our content Conductors Insulators and Semiconductors  then please don’t forget to check our other topics, Bloch’s Theorem and Kronig Penny Model