Rotational Kinetic Energy

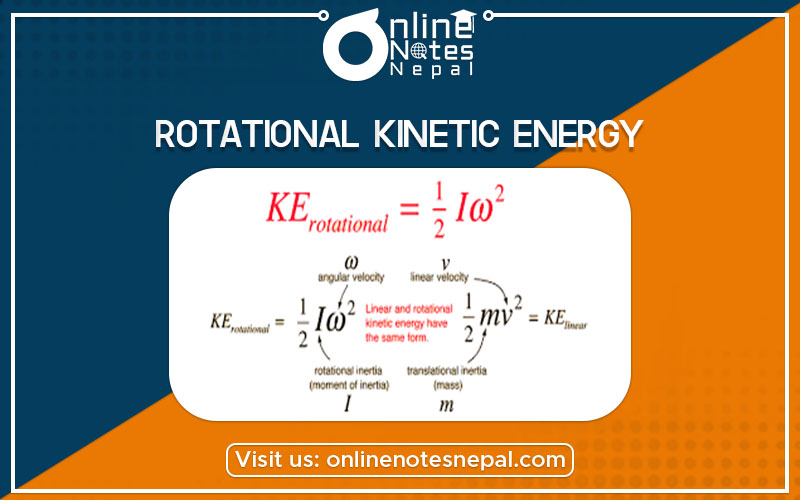
Rotational energy or angular energy is KE due to the rotation of an object and is part of its total KE.

In linear motion, the work done dW by force F in moving an object through displacement dx is dW=Fdx. In a similar way, in rotational motion F is replaced by τ and dx is replaced by dϴ.
That is,

Equation

By definition, the angular acceleration is given by the rate of the change of angular velocity

Equation

Substituting α for equation (i)

Equation

Also, Angular velocity ω is defined as the rate of change of angular displacement. Iω2

Equation

Substituting dϴ for equation (ii)

Equation

Where the quantity (1/2)Iω2 is called Rotational KE.
That is,

Equation

The expression for rotational kinetic energy can also be derived from linear kinetic energy as follows,
The linear kinetic energy is

Equation

But because of y = rω, the kinetic energy may be written as,

Equation

The moment of inertia of point mass is I = mr^2. Therefore,

Equation

Hence the expression for rotational kinetic energy in terms of I and ω is simply another form of linear kinetic energy.
Somebody like the earth has both translational and rotational motion. The earth rotates, about its axis, and move around the sun. In such a type of motion, the total energy is the sum of translational and kinetic energies.

Equation

The power is defined as the work done per unit time.
power= W/T