Spring Mass System

Picture

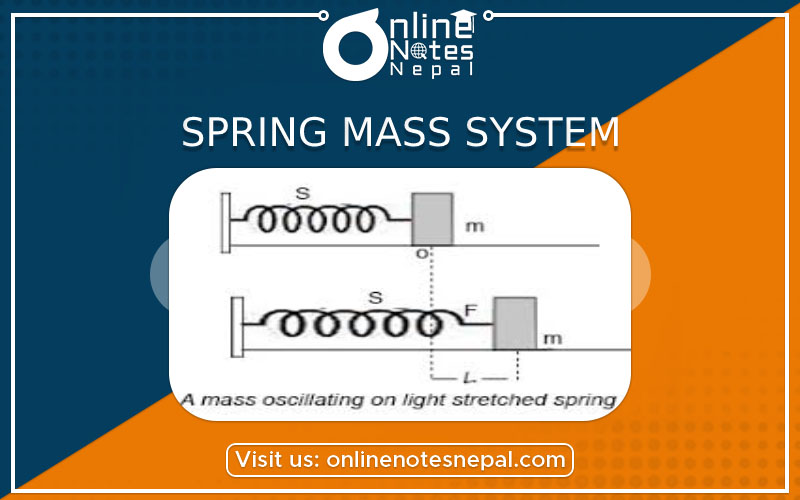
Let us find out the time period of a spring-mass system oscillating on a smooth horizontal surface as shown in the figure.
At the equilibrium position, the spring is relaxed. When the block is displaced through x towards the right, it experiences a net restoring force F = -kx towards left.
The negative sign shows that the restoring force is always opposite to the displacement. That is, when x is positive, F is negative, the force is directed to the left. When x is negative, F is positive, the force is directed to the right. Thus, the force always tends to restore the block to its equilibrium position x = 0.
so  F = -kx
Applying Newton’s Second Law,

Equation

Comparing the above equation with the standard equation, we get

Equation

This is the required expression for the time period of a mass-spring system. The mass of the spring is usually neglected in such type of problem because this expression shows that the time period of oscillation depends upon the attached to the spring.

Note that the time period is independent of the amplitude. For a given string constant, the period increases with the mass of the block – a more massive block oscillate more slowly. For a given block, the period decreases as k increases. A stiffer spring produces quicker oscillations.