Published by: BhumiRaj Timalsina
Published date: 22 Jun 2021
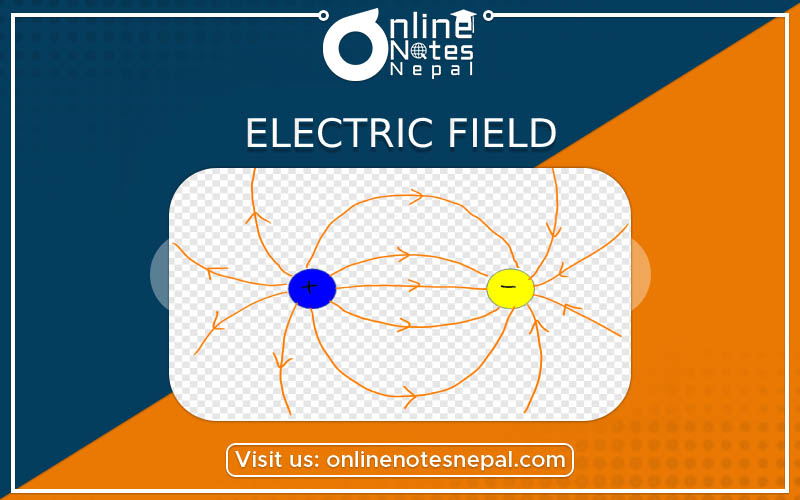
An electric field is a force that fills the space around every electric charge or group of charges. Electrical forces are similar to gravitational forces in that they act between things that are not in contact with each other. Electric fields are also analogous to magnetic fields resulting fromElectric fields are caused by electrical forces. forces acting upon magnetic substances or magnet poles. Electromagnetic waves have both an electric field and a magnetic field that are coupled to each other. Mathematically, the magnitude (or the strength) of an electric field at any point is defined by the force experienced by the charge at that point divided by the charge. This concept is written mathematically as E = F / q. Electric field strength is measured in units of newtons/coulomb. Electric fields are either static or dynamic.
Electric Charge is nothing but the amount of energy or electrons that pass from one body to another by different modes like conduction, induction, or other specific methods. This is a basic electric charge definition. There are two types of electric charges. They are positive charges and negative charges.
Charges are present in almost every type of body. All those bodies having no charges are the neutrally charged ones. We denote a charge y the symbol ‘q’ and its standard unit is Coulomb. Mathematically, we can say that a charge is the number of electrons multiplied by the charge on 1 electron. Symbolically, it is
Q = ne
where q is a charge, n is a number of electrons and e is a charge on 1 electron (1.6 × 10-19C). The two very basic natures of electric charges are
Like charges repel each other.
Unlike charges attract each other.
This means that while protons repel protons, they attract electrons. The nature of charges is responsible for the forces acting on them and coordinating the direction of the flow of them. The charge on electron and proton is the same in magnitude which is 1.6 × 10-19 C. The difference is only the sign that we use to denote them, + and -.
The electrostatic force of interaction acting between two stationary charges is given by
F = 1 / 4π εo q1q2 / r2
where q1, q2 is a magnitude of point charges, r is the distance between them and εo is the permittivity of free space.
Here, 1 / 4πεo = (10-7 N – s2 / C2)C2
Substituting value of c = 2.99792458 X 108 m/s,
We get 1 / 4πεo = 8.99 x 109N-m2/C2
In examples and problems we will often use the approximate value,
1 / 4πεo = 9 * 109N-m2/C2
The value of εo is 8.85 * 10-12 C2 / N-mC2.
If there is another medium between the point charges except for air or vacuum, then εo is replaced by εoK or εoεr or ε.
where K or εr is called the dielectric constant or relative permittivity of the medium.
K = εr = ε / εo
where, ε = permittivity of the medium.
For air or vacuum, K = 1
For water, K = 81
For metals, K = ∞
The electrostatic force acting per unit positive charge on a point in the electric field is called electric field intensity at that point.
Equation
Electric field intensity E =
Its SI unit is NC-1 or Vim and its dimension is [MLT-3 A-1].
It is a vector quantity and its direction is in the direction of electrostatic force acting on a positive charge.
Electric field intensity due to a point charge q at a distance r is given by
E = 1 / 4π εo q / r2
Equation
The physical quantity that drives electric charge in an electric field is called electric potential. The electric potential at a point inside an electric field is defined as the amount of work done in bringing unit positive charge from infinity to that point (without acceleration).
Consider a system of two point charges in which positive test charge q’ moves in the field produced by stationary point charge q shown below in the figure.
Picture
Charge q is fixed at point P and is displaced from point R to S along a radial line PRS shown in the figure.
Let r1 be the distance between points P and R and r2 be the distance between P and S.
The magnitude of the force on positive test charge as given by Coulomb’s law is
Equation
If q’ moves towards S through a small displacement dr then work done by this force in making the small displacement dr is
dW=F·dr
Equation
Total work done by this force as test charge moves from point R to S i.e., from r1 to r2 is,
Equation
or
Equation
Thus for this particular path work done on test charge q’ depends on endpoints, not on the path taken.
Work done W in moving the test charge q’ from point R to S is equal to the change in potential energy in moving the test charge q’ from point R to S. Thus,
W=U(r1)-U(r2) (4)
where
Equation
is the electrostatic potential energy of test charge q’ when it is at point R and
Equation
is the potential energy of test charge q’ when it is at point S.
The electrostatic potential difference between two points in an electric field is defined as the amount of work done in moving a unit positive test charge from one point to the other point against of electrostatic force without any acceleration (i.e. the difference of electrostatic potentials of the two points in the electric field).
Equation
where, is work done in taking charge q0 from A to B against electrostatic force.
Also, the line integral of the electric field from initial position A to final position B along any path is termed as a potential difference between two points in an electric field, i.e.
Equation
An expression for the potential difference between two point r1 and r2 from +Q;
An electric potential (also called the electric field potential or the electrostatic potential) is the amount of electric potential energy that a unitary point electric charge would have if located at any point in space and is equal to the work done by an electric field in carrying a unit positive charge from infinity.
Consider a point charge +Q placed at point O in free space as shown in free space. It is desired to find the electric potential at point A at a distance r from O, i.e. OA = r
If W ∞A is the amount of work done, the potential at a point is given by
VA = W∞ A……………………1
To calculate W ∞A, consider that at any instant, the test charge is at point P which is at a distance X from O such that OP = X.
Equation
If the test charge is moved dx from P to Q
Equation
The total amount of work done in bringing the test charge from infinity to A is given by integrating Eq 3, so,
Equation
This is the electric potential at point A which is at a distance r from the point charge +Q.