Moment of Inertia

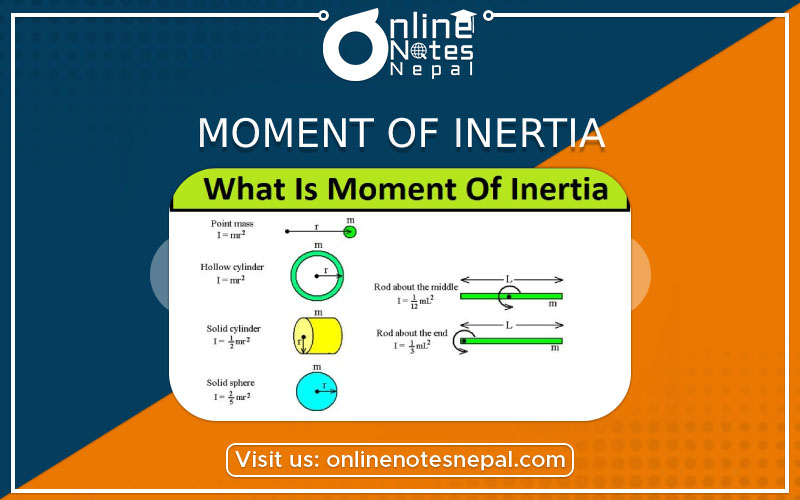
The properties of the rotational body about the axis of rotation due to which it remains in the original state about the axis of rotation is a moment of inertia. It is also called rotational inertia. It is denoted by ‘I’ and is a scalar quantity.

Torque (τ )

It is defined as a turning effect of force or moment of force which is denoted by τ. Mathematically, torque is a product of the force applied and the perpendicular distance between the point of rotation and line of action of the force. If F be the force applied and r be the distance from point of rotation to the point of action of the force then,
τ = τr * F
Or τ = rFsinϴ
If ϴ = 90,
τ = r * F

Relation Between Torque and Moment of Inertia

The rotation of point mass is attached with one end of the massless rigid rod of length ‘r’ about point ‘O’ as shown in the figure. Suppose force ‘F’ is applied at a point ‘P’ to the point mass in the direction making angle ϕ with a rigid rod. The force F has the following two orthogonal components
Fr =Fcos ϕ which acts as a long rigid rod on outward. It has no work
FT=Fsin ϕ which acts along tangent and produce rotational motion with tangential acceleration aT
Hence, from the second law of motion
F = maT ……….(i)

 

FT = Fsin ϕ……..(ii)
We have from equation (i) and (ii),

Fsinϕ = maT
If α be the angular acceleration then,
Fsinϕ = mrα
(since a=rα)
Now, multiplying by ‘r’ on both sides,
Frsin ϕ = mr2α
Or, hF = mr2α……(iii)                                                                                                                                 
(since h= rsinϕ )
In equation(iii) the quantity hF represents the product of the force applied and the perpendicular distance between the force applied and the perpendicular distance between the point of rotation and line of action of the force. Hence it is called torque.
τ=Iα

I=mr^2