Carrier Density and Fermi Levels

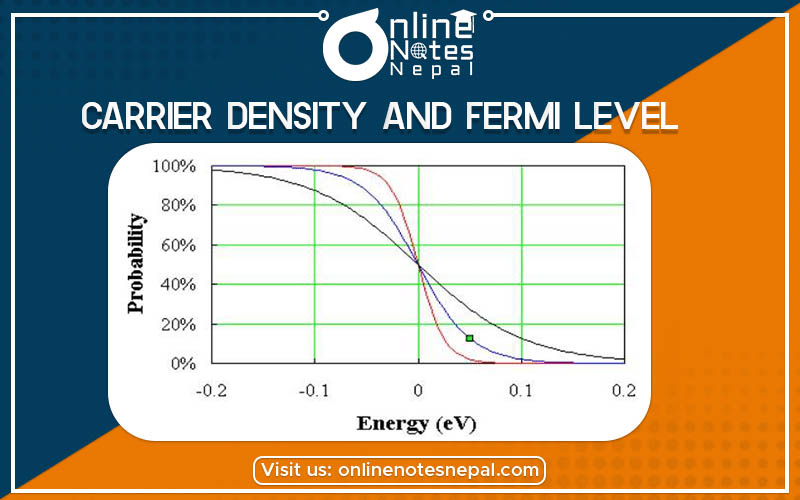
Carrier Density and Fermi Levels of impure semiconductors are two of the other major factors that help to determine conductivity. The presence of the impurity state significantly affects the number of electrons in the conduction band or holes in the valence band. They affect the position of the Fermi Level.

In the n-type semiconductor, electrons can be excited into the conduction band from the donor level as well as from the valence band. We know that at equilibrium the electrons ‘n’ in the conduction band must be equal to the number of holes in the valence band plus the number of donor impurity atoms per unit volume. These have been ionized Nd+.

The equation for Carrier Density and Fermi Level

i.e. n = p + Nd+         ……………………(1)

Let Nd be the impurity atoms per unit volume. There will be Nd electrons in the energy level Ed that makes the transition to the conduction band. If we multiply Nd by the probability that an electron will not be at Ed,

We get,

Nd+ = Nd [1-f(Ed)]  ………………….. (2)

Using equation (2) in (1),

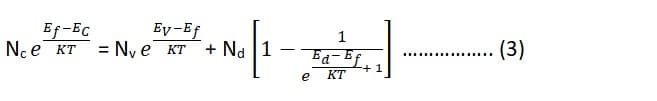
Where,

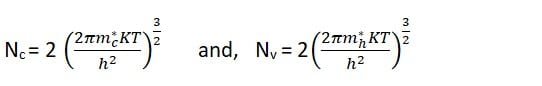
At low temperature, the Fermi Level lies halfway between Ed and the bottom of conduction band i.e.

n=p

As the temperature increases, Ef approaches the value for the intrinsic semiconductor.

In the p-type semiconductor, acceptor levels of energy Ea exist very close to the top of the valence band. At equilibrium the no. of holes in the valence band ‘p’ must be equal to the no. of electrons in conduction band plus the no. of acceptor impurity atoms per unit volume that are ionized by the Na–.

i.e.    p = n + Na–   ……………….. (4)

Let Na– be the acceptor impurity atoms per unit volume. Then Na– can be obtained using Fermi-Dirac function, i.e.,

Na– = Na f(Ea)

Using equation (5) in (4), we get,

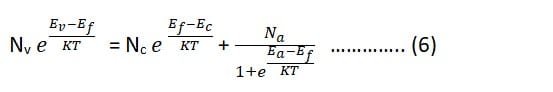
At low temperature, the Fermi level lies halfway between Ea and the top of the valence band i.e.

Equation

As the temperature increases, the Ef approaches the value for the semiconductor.