Angular Momentum

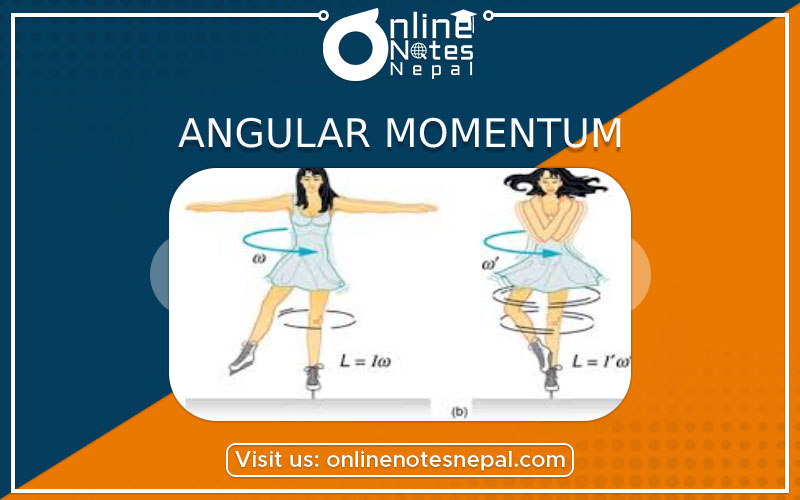
It is conserved, i.e. the initial momentum is equal to the final momentum when no external torque is applied to the system.

The law of conservation of angular momentum states that:
“When the net external torque acting on a system about a given axis is
zero, the total angular momentum of the system about that axis remains constant.”

Proof

Mathematically,

Equation

Angular momentum is defined as:

Equation

Differentiating both sides with respect to “t”

Equation

which is the required equation
This expression states that the torque acting on a particle is the time rate of change of its angular momentum. If the net external torque on the particle is zero and then integrating both sides we get,

Equation

Differentiating both sides with respect to “t”

Equation

Applications:

• Electric generators,
• Aircraft engines, etc

Examples:

• Consider an ice skater who begins to spin such that his arms are spread out as far as possible and is parallel to the ice. What happens to the angular velocity of the skater when he pulls his arms inwards and when he raises his arms vertically?

  The angular velocity of the skater increases when he pulls his arms inwards because the moment of inertia is lowered. And his angular velocity stays the same when he raises his arms vertically because the distribution of radius of mass does not change.

• Where can we find the center of mass of two particles with equal mass?

  The center of mass of two particles with equal mass is found in the midway between them.