Types of K-maps

According to the no. of used variables in a question and the need for a problem in the simplification of Boolean functions, there are some of the types of K-maps. They are:

• Two-Variable K-map

We know that for ‘n’ variables, 2n squares are required. So, there are four minterms for two-variable K-maps i.e. 22 =4. Hence, this map consists of 4 squares.

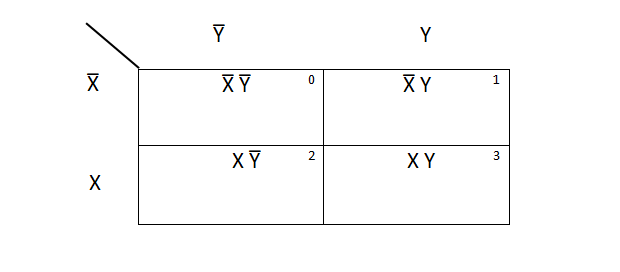
For example:
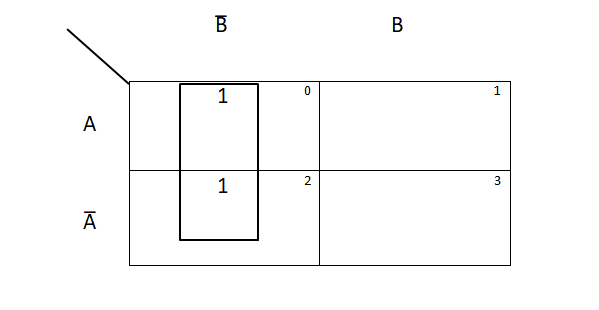
Simplification of Y = A̅ B̅ + A B̅ using K – map

• Three variable K-map

There are 8 minterms for three variable k-maps i.e. 2n = 23 = 8.

Hence, the map consists of 8 squares.

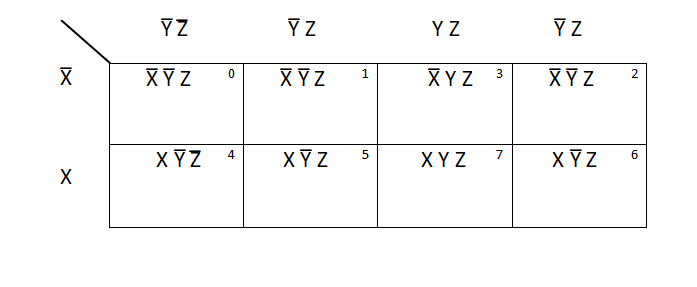
For example:

Simplification of F = X̅ Y Z + X̅ Y Z̅ + X Y̅ Z̅ + X Y̅ Z

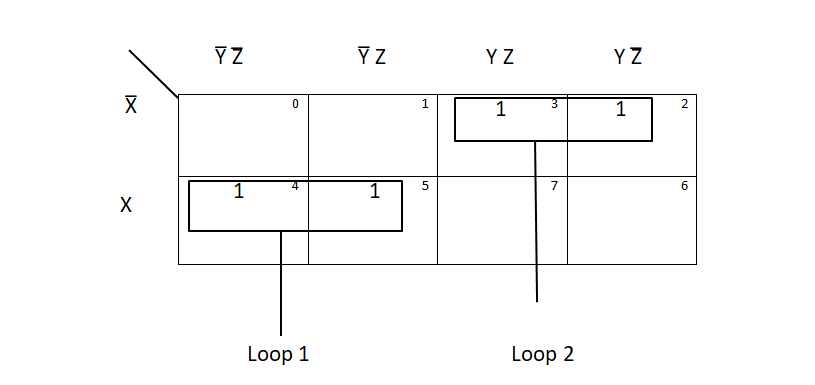
Therefore, F = X̅ Y + X Y̅ is the simplified expression. There are two loops in this table. 1 and 3 are grouped together & 4 and 5 are grouped together.

 

• Four Variable K-map

There are 16 minterms for 4 variable K- map, i.e. 2n = 24 = 16.

Hence the map of 4 variables consists of 16 squares altogether.

 

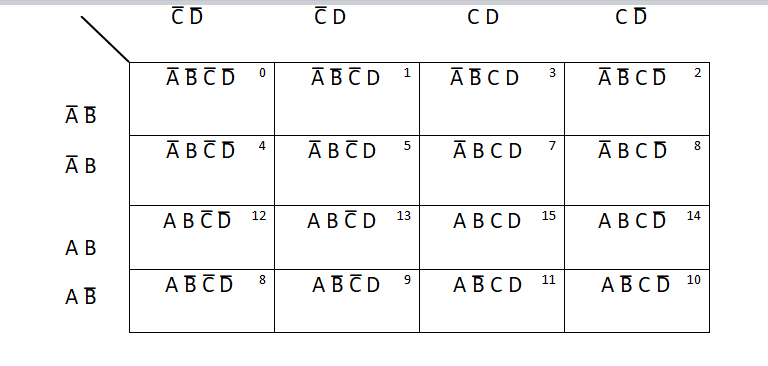
For example:

Simplification of F = A̅ B C̅ D + A B C̅ D + A̅ B C D + A B C D + A̅ B̅ C̅ D̅

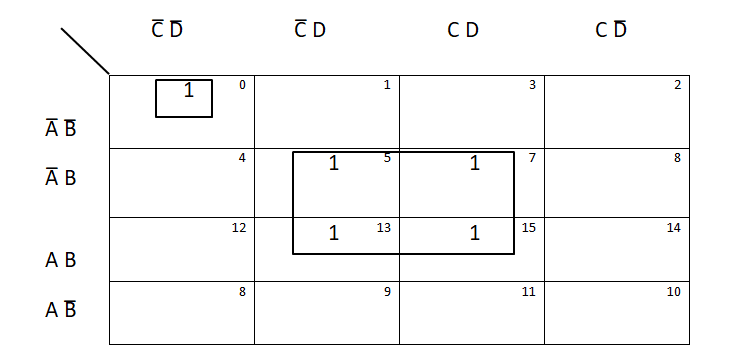
There are 2 loops. 0 is looped alone and 5, 7, 13, and 15 are kept in the loop together.

Therefore, F = A̅ B̅ C̅ D̅ + BD is the required solution.