Boolean algebra

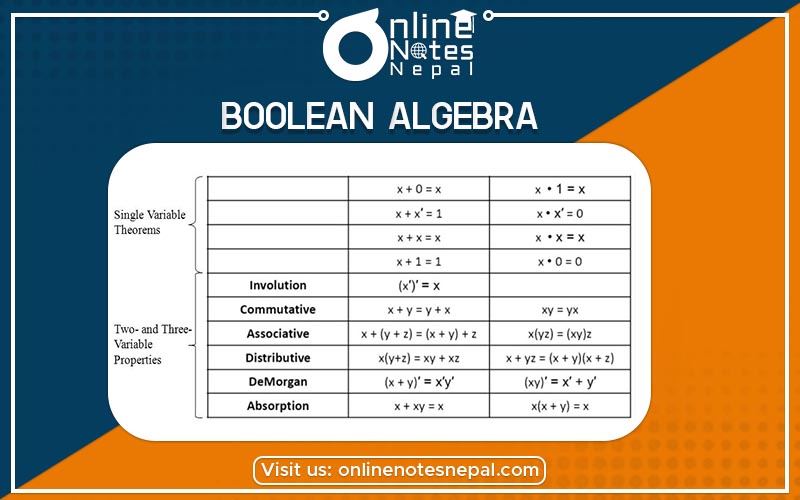
Boolean algebra is the method of expressing logic in a mathematical context. It is a form of symbolic logic in the computer. Boolean Variable shows the values of variables as true or false. True value is denoted by 1 and a false value is denoted by 0 that are the binary numbers as well. These two values are expressed by the Boolean operators AND, OR, and NOT. They are fundamental to the development of digital electronics. These are mainly used in solving logical equations like in the set theory and statistics.

The terminology

If F=(a, b, c) = a’bc+ abc’+ab+ c be a Boolean function, then,

• Variable: Represents a value 0 or 1 which says either false or true respectively.
• Literal: There are nine literals; a’, b, c, a, b, c’, a, b, &c in the equation above.
• Product terms: Product of literals, four product terms a’bc, abc’, ab, c is above.
• Sum of products: The sum of the product is; F=(a+b)c +d which is not.

Postulates

We can obtain the postulates by examining the basic logical operators which are AND, OR & NOT.

• From AND operation

0.0 = 0
0.1 = 0
1.0 = 0
1.1 = 1

• From OR operation

0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 1

• From NOT operation

0̅ = 1
1̅ = 0

Theorems of Boolean Functions:

• Law of Union

A+1 = 1
A+0 = A

• Law of Identity

X = X
X̅ = X̅

• Idempotent Law

A+(B+C) = A+B+C

• Commutative Law

X.Y = Y.X
X+Y = Y+X

• Associative Law

X (YZ) = (XY) Z
(X+Y)+Z = X+(Y+Z)

• Distributive Law

X(Y+Z) = XY+XZ
X+YZ = XY+XZ

• Complementary law

X̿ = X
X+X̅ = 1

• De-Morgan’s Law

X͞Y = X̅ + Y̅
(X+Y) ̅ = X̅ +Y̅

• Absorption Theorem

X+XY = X
X(X+Y) =X

• Law of common identities

A.(A̅ +B) = AB
A+(A̅B)=A+B

• Double Negative Law

A.A = A
A+A = A