Adders

Digital computers perform a variety of information-processing tasks. Among the basic functions encountered are the various arithmetic operations. The most basic arithmetic operation, no doubt, is the addition of two binary digits. It is done by adders.

Adders are basically of two types;

1. Half-Adders

• A combinational circuit that performs the addition of two bits is called a half-adder.
• The circuit needs two inputs and two outputs. The input variables designate the augend (x) and addend (y) bits; the output variables produce the sum (S) and carry (C).
• Now we formulate a Truth table to exactly identify the function of half-adder.

Design of half-adder:

Input: 2 (let x and y)
Output: 2 (let C for Carry and S for Sum)
Truth table:

X	Y	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

The simplified Boolean functions for the two outputs can be obtained directly from the truth table. The simplified sum of products
expressions are:

S = x'y + xy'
C = xy

Implementation:

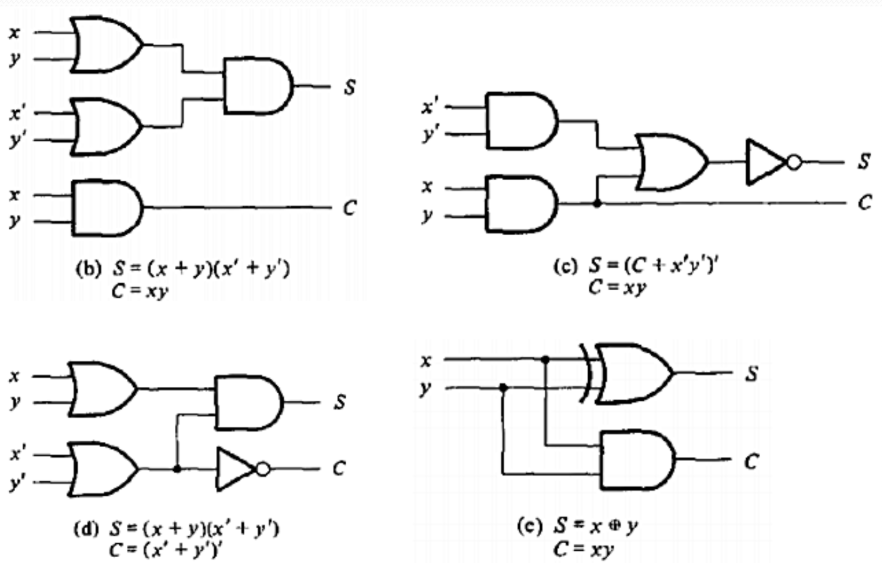
Other realizations and implementations of Half-adders are:

 

2. Full-Adders

• A full-adder is a combinational circuit that forms the arithmetic sum of three input bits.
• It consists of three inputs and two outputs. Two of the input variables, denoted by x and y, represent the two significant bits to be added. The third input, z, represents the carry from the previous lower significant position.

Design:

Input: 3(Let x, y, z )
Output: 2(Let C for carry and S for sum)
Truth Table:

X	Y	Z	C	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
0	1	0	0	1
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0

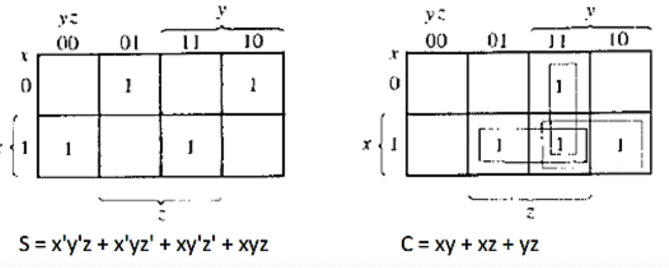
Boolean functions with simplification by K-map:

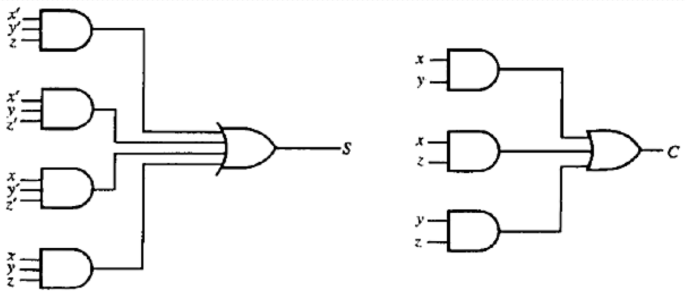
Implementation:

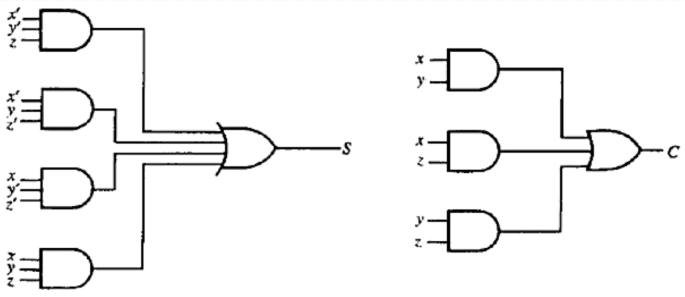
Fig: Implementation of a full-adder in terms of the sum of products.

 

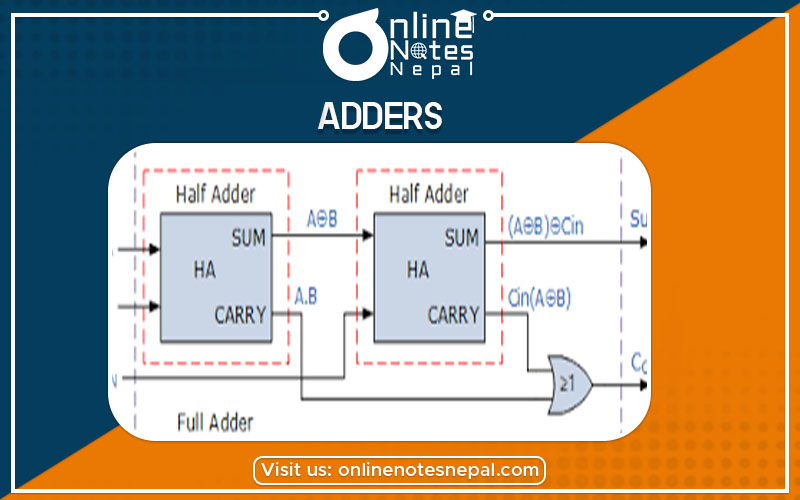
A full-adder can be implemented with two half-adders and one OR gate.

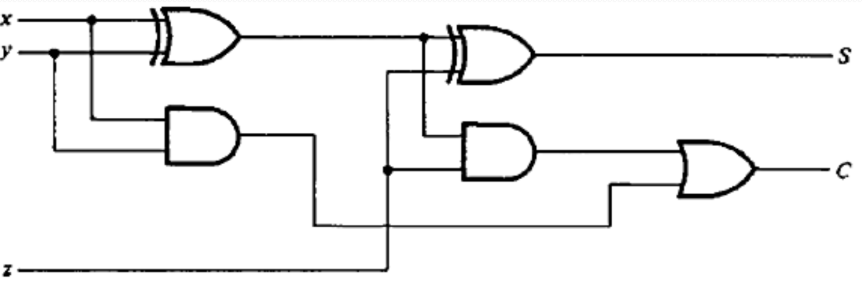
Fig: Implementation of a full-adder with 2 half-adders and an OR gate

Here, The S output from the second half-adder is the exclusive-OR of z
and the output of the first half-adder, giving:
S = z ⊕ (x ⊕ y)                                                    C = z (x ⊕ y) + xy
= z'(xy' + x'y) + z(xy' + x'y)'                                     = z(xy' + x'y) + xy
= z'(xy' + x'y) + z(xy + x'y')                                      = xy'z + x'yz + xy
= xy'z' + x'yz' + xyz + x'y'z

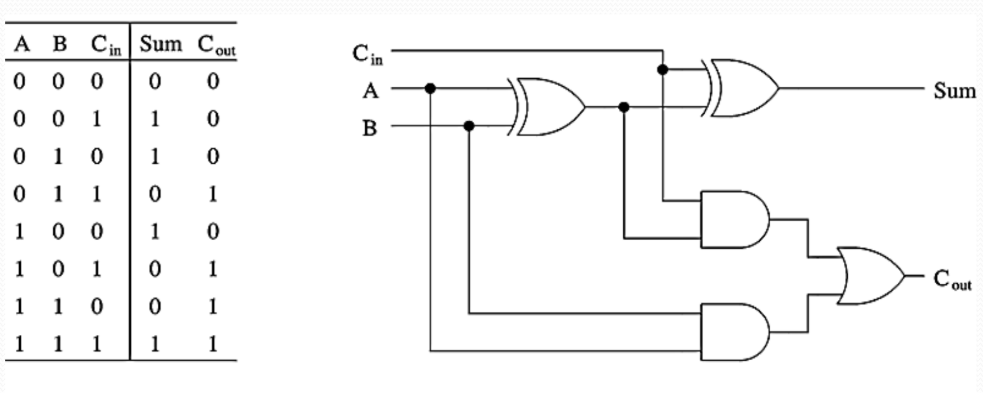
Fig: Full adder truth table and implementation