Published by: Nuru
Published date: 22 Jun 2021
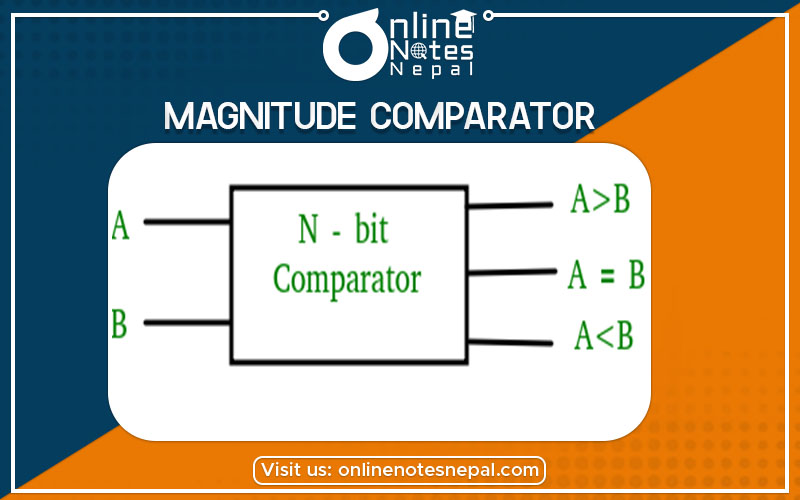
A Magnitude comparator is a combinational circuit that compares two numbers, A and B, and determines their relative magnitudes. The outcome of the comparison is specified by three binary variables that indicate whether A > B, A = B or A < B.
Consider two numbers, A and B, with four digits each. The coefficients of the numbers with descending significance as follows:
A = A3A2A1A0
B = B3B2B1B0
Where each subscripted letter represents one of the digits in the number, the two numbers are equal if all pairs of significant digits are equal, i.e., if A3= B3 and A2= B1 and A1= B1 and A0= B0
When the numbers are binary, the digits are either 1 or 0 and the equality relation of each pair of bits can be expressed logically with an equivalence function obtained from the truth table:
0
| A | B | X |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
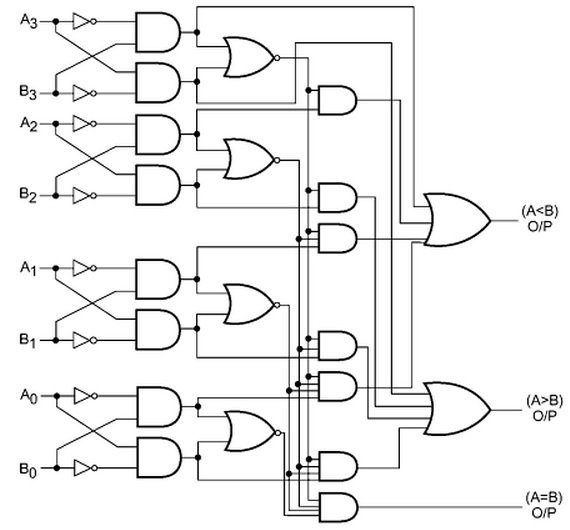
Fig: 4-bit Magnitude Comparator
Xi = AiBi + Ai'Bi'
Where,
Xi= 1 only if the pair of bits in position i are equal, i.e., if both are 1's or both are 0's
i = 0, 1, 2, 3
(A = B)
For the equality condition to exist, all Xi variables must be equal to 1.This dictates an AND operation of all variables:
(A = B) = X3 X2X1 X0
The binary variable (A = B) is equal to 1 only if all pairs of digits of the two numbers are equal.
(AB)
To determine if A is greater than or less than B, we check the relative magnitudes of pairs of significant digits starting from the most significant position. If the two digits are equal, we compare the next lower significant pair of digits. This comparison continues until a pair of unequal digits is reached.
A > B: If the corresponding digit of A is 1 and that of B is 0.
A < B: If the corresponding digit of A is 0 and that of B is 1.
The sequential comparison can be expressed logically by the following two Boolean functions:
(A > B) = A3B3' + X3A2B2' + X3X2A1B1' + X3X2X1A0B0'
(A < B) = A3'B3 + X3A2'B2 + X3 X2A1'B1 + X3X2X1A0'B0
The symbols (A > B) and (A < B) are binary output variables that are equal to 1 when A > B or A < B respectively.