Multilevel Circuits

There are two multilevel circuits that we are going to learn on this topic.

1. Multi-level NAND circuits

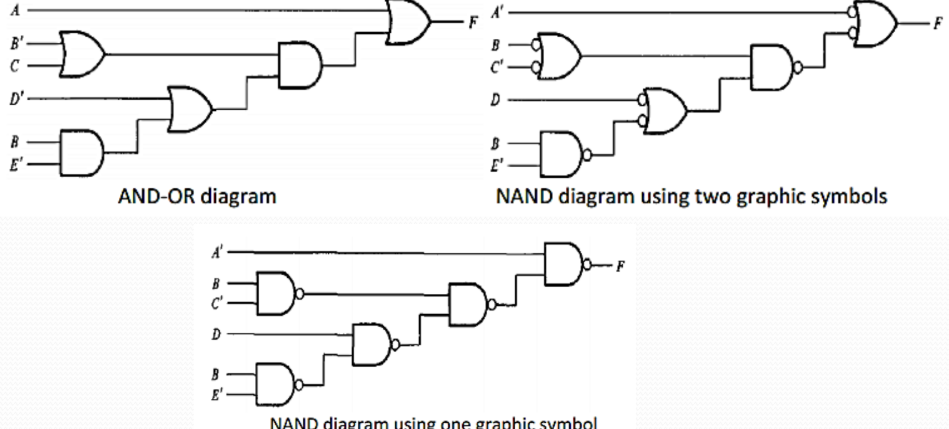
To implement a Boolean function with NAND gates we need to obtain the simplified Boolean function in terms of Boolean operators and then convert the function to NAND logic. The conversion of an algebraic expression from AND, OR, and complement to NAND can be done by simple circuit-manipulation techniques that change AND- OR diagrams to NAND diagrams.

To obtain a multilevel NAND diagram from a Boolean expression, proceed as follows:

1. From the given Boolean expression, draw the logic diagram with AND, OR, and inverter gates. Assume that both the normal and complement inputs are available.
2. Convert all AND gates to NAND gates with AND-invert graphic symbols.
3. Convert all OR gates to NAND gates with invert-OR graphic symbols.
4. Check all small circles in the diagram. For every small circle that is not compensated by another small circle along the same line, insert an inverter (one-input NAND gate) or complement the input variable.

Example: F = A + (B' + C) (D' + BE ')

2. Multi-level NOR circuits

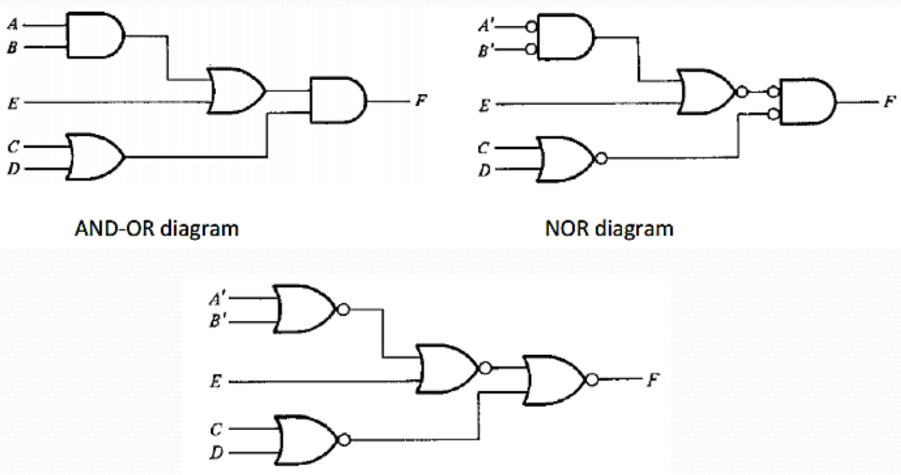
The NOR function is the dual of the NAND function. For this reason, all procedures and rules for NOR logic form a dual of the corresponding
procedures and rules developed for NAND logic. Similar to NAND, NOR has also two graphic symbols: OR-invert and invert-AND symbol. The procedure for implementing a Boolean function with NOR gates is similar to the procedure outlined in the previous section for NAND
gates:

1. Draw the AND-OR logic diagram from the given algebraic expression. Assume that both the normal and complement inputs are available.
2. Convert all OR gates to NOR gates with OR-invert graphic symbols.
3. Convert all AND gates to NOR gates with invert-AND graphic symbols.
4. Any small circle that is not compensated by another small circle along the same line needs an inverter or the complementation of the input variable.

Example: F = (AB + E) (C + D)