Published by: Dikshya
Published date: 09 Jul 2023
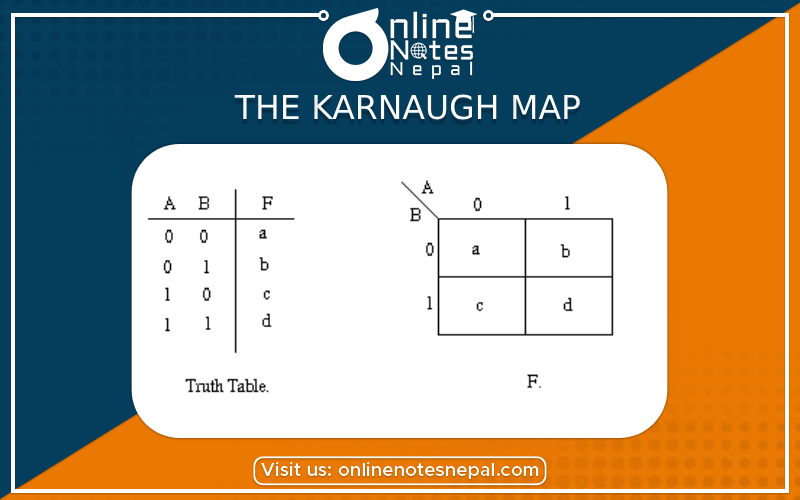
- The Karnaugh map, also known as the K-map, is a graphical representation technique used in digital logic design to simplify Boolean algebra expressions and minimize logic functions. It provides a systematic method for finding the minimal expression of a logical function and optimizing digital circuits.
- The Karnaugh map consists of a grid of cells, with each cell representing a unique combination of input variables. The number of rows and columns in the grid depends on the number of input variables in the logic function. The cells in the map are arranged in a way that adjacent cells differ by only one variable, either in complemented (inverted) or uncomplemented form.
- To use the Karnaugh map, you start by writing down the truth table of the logic function you want to simplify. Then, you fill in the Karnaugh map by mapping the output values from the truth table to the corresponding cells in the map. Each cell in the map represents a minterm or maxterm of the function.
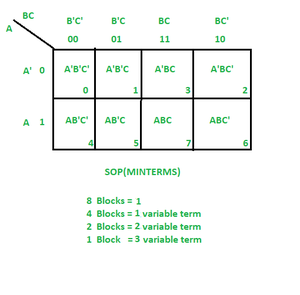
- Next, you look for groups of adjacent 1s or 0s in the map. These groups are called implicants and represent terms in the simplified expression. You can combine adjacent cells into larger groups (2, 4, 8, etc.) by combining variables that change between the cells while keeping the remaining variables constant.
- Once you have identified all the implicants, you select the minimal set of implicants that cover all the 1s or 0s in the map. This selection process is done by choosing the implicants that cover the most cells while minimizing the number of variables involved. The resulting implicants form the simplified Boolean expression for the logic function.
- The Karnaugh map is a valuable tool in digital logic design as it provides a visual representation of the logic function and facilitates the simplification process. It helps reduce the complexity of logical expressions, minimize circuit size, and improve circuit performance.
- The Karnaugh map has several uses in digital logic design. Some of the main applications and benefits of using Karnaugh maps include:
- Simplification of Boolean expressions: Karnaugh maps are primarily used to simplify Boolean algebra expressions. They provide a visual representation of the logic function, making it easier to identify patterns and groups of adjacent cells. By grouping cells with the same output values, you can reduce the number of terms and variables in the expression, leading to a simpler and more compact representation.
- Minimization of logic functions: Karnaugh maps help in minimizing logic functions by identifying the essential prime implicants. These implicants are the smallest groups of adjacent cells that cover all the 1s or 0s in the map. By selecting the minimal set of implicants, you can derive the simplest possible expression for the logic function, reducing the number of gates and improving circuit efficiency.
- Circuit optimization: By simplifying Boolean expressions, Karnaugh maps aid in optimizing digital circuits. Smaller and simpler expressions lead to fewer logic gates, shorter signal propagation paths, and reduced power consumption. Circuit optimization helps improve overall performance, reduce costs, and enhance reliability.
- Error detection and correction: Karnaugh maps can be used in error detection and correction techniques, such as parity checking and Hamming codes. By analyzing the patterns and combinations of cells in the map, you can identify errors and determine the correct output values.
- Combinational and sequential circuit design: Karnaugh maps are widely used in the design of both combinational and sequential logic circuits. They assist in designing circuits for functions with multiple inputs and outputs, allowing designers to create efficient and reliable circuits.
- Education and learning: Karnaugh maps serve as a useful educational tool for teaching and learning digital logic design concepts. They provide a visual and intuitive approach to understanding Boolean algebra, simplification techniques, and logic function optimization.