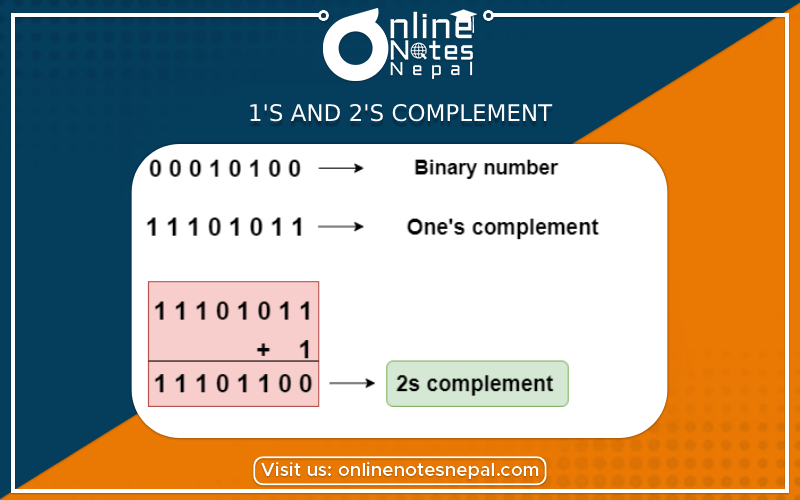
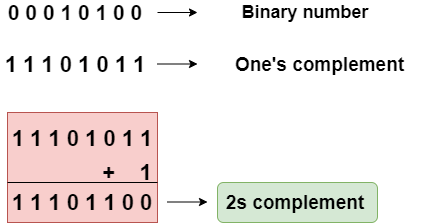1's and 2's complement:

The 1's complement and 2's complement are mathematical techniques used to represent negative numbers in binary form. They are commonly employed in computer systems, particularly for signed integer representation and arithmetic operations. Let's explore each technique:

1. 1's Complement:

The 1's complement of a binary number is obtained by flipping all the bits, i.e., changing 0s to 1s and 1s to 0s. To represent a negative number using 1's complement, the most significant bit (MSB) is used as the sign bit. If the sign bit is 0, the number is positive, and if the sign bit is 1, the number is negative.

For example:

a. Positive number: 0101 (decimal 5)

b. Negative number: 1010 (1's complement of 0101)

To perform addition and subtraction using 1's complement, the following rules apply:

- Addition: Add the numbers as you would with unsigned binary numbers. If there is a carry out of the MSB, add it back to the least significant bit (LSB). If there is a carry into the MSB, it is accounted for by adding it to the result.

- Subtraction: Perform the addition of the minuend (number being subtracted from) and the 1's complement of the subtrahend (number being subtracted). Follow the same rules as addition, including handling carry-in and carry-out.

1's complement has a drawback known as the "1's complement overflow" issue, where the result can have an extra carry that needs to be handled separately.

2. 2's Complement:

The 2's complement of a binary number is obtained by adding 1 to the 1's complement of the number. Similar to the 1's complement, the MSB is used as the sign bit.

For example:

a. Positive number: 0101 (decimal 5)

b. Negative number: 1011 (2's complement of 0101)

To perform addition and subtraction using 2's complement, the following rules apply:

- Addition: Add the numbers as you would with unsigned binary numbers. Ignore any carry out of the MSB.

- Subtraction: Perform the addition of the minuend and the 2's complement of the subtrahend. Ignore any carry out of the MSB.

2's complement offers a more convenient and efficient representation for negative numbers since it eliminates the need to handle the 1's complement overflow separately. It also has the property that the range of representable values is symmetric around zero, making it easier to perform arithmetic operations.

In computer systems, the 2's complement is the most commonly used technique for representing negative numbers due to its simplicity and efficiency in arithmetic operations.