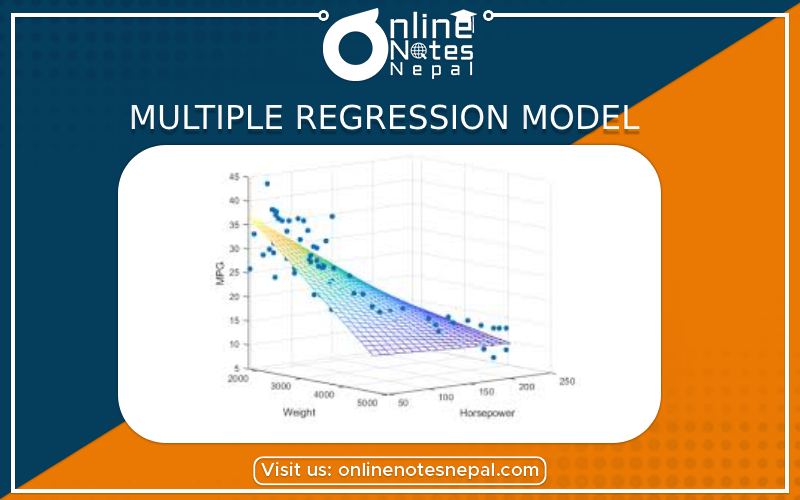
Title: Multiple Regression Model

Introduction: The multiple regression model is a statistical method used to examine the relationship between a dependent variable and two or more independent variables. It is an extension of simple linear regression, which deals with just one independent variable. Multiple regression allows us to analyze how several factors influence the outcome variable simultaneously, providing a more comprehensive understanding of the relationships between variables.

Mathematical Formulation: In the multiple regression model, we represent the dependent variable (Y) as a linear combination of two or more independent variables (X1, X2, ..., Xn) and an error term (ε). Mathematically, the model can be written as:

Y = β0 + β1X1 + β2X2 + ... + βn*Xn + ε

Where:

• Y represents the dependent variable (the outcome we want to predict).
• β0 is the intercept, the value of Y when all independent variables are zero.
• β1, β2, ..., βn are the coefficients or regression weights, representing the impact of each independent variable on Y.
• X1, X2, ..., Xn are the independent variables.
• ε is the error term, accounting for the unexplained variability in Y.

Assumptions of Multiple Regression:

1. Linearity: The relationship between the dependent variable and the independent variables is assumed to be linear.
2. Independence: The observations are independent of each other.
3. Normality: The error term (ε) is normally distributed.
4. Homoscedasticity: The variance of the error term is constant across all levels of the independent variables.
5. No Multicollinearity: The independent variables are not highly correlated with each other.

Estimating Coefficients: The coefficients (β0, β1, β2, ..., βn) are estimated using a method called Ordinary Least Squares (OLS). The goal of OLS is to minimize the sum of squared differences between the observed values of the dependent variable and the values predicted by the regression equation.

Interpreting Coefficients: The coefficients indicate the change in the dependent variable for a one-unit change in the corresponding independent variable, assuming all other variables remain constant. For example, if β1 is 0.5, it means that a one-unit increase in X1 is associated with a 0.5-unit increase in Y.

Model Fit and R-squared: R-squared (R²) is a measure of the goodness-of-fit of the regression model. It represents the proportion of the total variation in the dependent variable that is explained by the independent variables. R-squared values range from 0 to 1, where 0 indicates no fit, and 1 indicates a perfect fit. However, high R-squared does not guarantee that the model is appropriate or that the independent variables cause the changes in the dependent variable.

Hypothesis Testing: Statistical tests can be conducted to assess the significance of individual coefficients. The null hypothesis (H0) states that the coefficient is equal to zero, indicating that the corresponding independent variable has no effect on the dependent variable. A low p-value (typically less than 0.05) rejects the null hypothesis and suggests that the variable is significant in explaining the variation in the dependent variable.

Model Evaluation: To ensure the reliability and validity of the multiple regression model, it is essential to evaluate its assumptions and diagnose any potential issues. Common diagnostic techniques include residual analysis, checking for multicollinearity, and assessing influential data points.

Conclusion: The multiple regression model is a powerful tool for understanding and predicting the relationships between multiple variables. By estimating coefficients and examining their significance, researchers and analysts can gain valuable insights into the factors that influence the dependent variable. However, it is crucial to interpret the results with caution and verify the model's assumptions for accurate and reliable conclusions.