Published by: Zaya
Published date: 25 Jun 2021

Fission is the splitting of a heavy nucleus into lighter nuclei and fusion is the combining of nuclei. Protons and neutrons make up a nucleus, which is the foundation of nuclear science. Fission and fusion involve the dispersal and combination of elemental nucleus and isotopes, and part of nuclear science is to understand the process behind this phenomenon. Adding up the individual masses of each of these subatomic particles of any given element will always give you a greater mass than the mass of the nucleus as a whole. The missing idea in this observation is the concept called nuclear binding energy. Nuclear binding energy is the energy required to keep the protons and neutrons of a nucleus intact, and the energy that is released during nuclear fission or fusion is nuclear power. There are some things to consider, however. The mass of an element’s nucleus as a whole is less than the total mass of its protons and neutrons. The difference in mass can be attributed to the nuclear binding energy. The nuclear binding energy is considered as mass, and that mass becomes “missing”. This missing mass is called a mass defect, which is nuclear energy, also known as the mass released from the reaction as neutrons, photons, or any other trajectories. In short, mass defect and nuclear binding energy are interchangeable terms.
Nuclear fission is the splitting of a heavy nucleus into two lighter ones. Fission was discovered in 1938 by the German scientist's Otto Hahn, Lise Meitner, and Fritz Strassmann, who bombarded a sample of uranium with neutrons in an attempt to produce new elements with Z > 92. They observed that lighter elements such as barium (Z = 56) were formed during the reaction, and they realized that such products had to originate from the neutron-induced fission of uranium-235:

This hypothesis was confirmed by detecting the krypton-92 fission product. As discussed in Section 20.2, the nucleus usually divides asymmetrically rather than into two equal parts, and the fission of a given nuclide does not give the same products every time.
In a typical nuclear fission reaction, more than one neutron is released by each dividing nucleus. When these neutrons collide with and induce fission in other neighbouring nuclei, a self-sustaining series of nuclear fission reactions known as a nuclear chain reaction can result (Figure 21.6.2).
For example, the fission of 235U releases two to three neutrons per fission event. If absorbed by other 235U nuclei, those neutrons induce additional fission events, and the rate of the fission reaction increases geometrically. Each series of events is called a generation. Experimentally, it is found that some minimum mass of a fissile isotope is required to sustain a nuclear chain reaction; if the mass is too low, too many neutrons can escape without being captured and inducing a fission reaction. The minimum mass capable of supporting sustained fission is called the critical mass. This amount depends on the purity of the material and the shape of the mass, which corresponds to the amount of surface area available from which neutrons can escape, and on the identity of the isotope. If the mass of the fissile isotope is greater than the critical mass, then under the right conditions, the resulting supercritical mass can release energy explosively. The enormous energy released from nuclear chain reactions is responsible for the massive destruction caused by the detonation of nuclear weapons such as fission bombs, but it also forms the basis of the nuclear power industry.
Nuclear fusion, in which two light nuclei combine to produce a heavier, more stable nucleus, is the opposite of nuclear fission. As in the nuclear transmutation reactions discussed in Section 20.2, the positive charge on both nuclei results in a large electrostatic energy barrier to fusion. This barrier can be overcome if one or both particles have sufficient kinetic energy to overcome the electrostatic repulsions, allowing the two nuclei to approach close enough for a fusion reaction to occur. The principle is similar to adding heat to increase the rate of a chemical reaction. As shown in the plot of nuclear binding energy per nucleon versus the atomic number in Figure 21.6.3, fusion reactions are most exothermic for the lightest element. For example, in a typical fusion reaction, two deuterium atoms combine to produce helium-3, a process known as deuterium–deuterium fusion (D–D fusion):
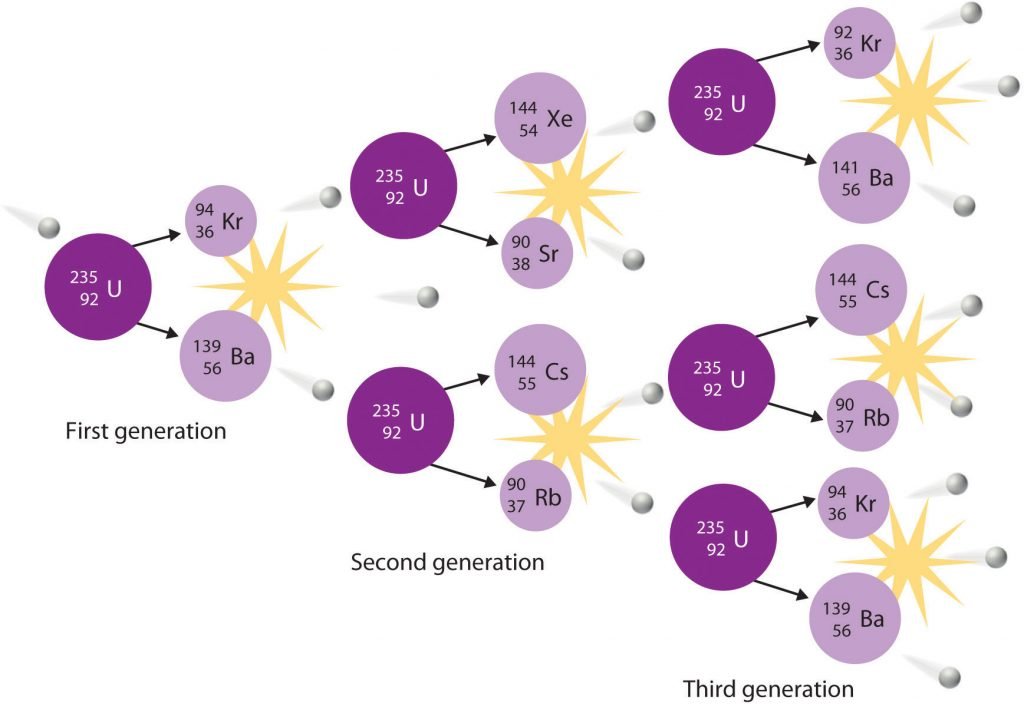
Figure 20.6. Because each neutron released can cause the fission of another 235U nucleus, the rate of a fission reaction accelerates geometrically. Each series of events is a generation.
In another reaction, a deuterium atom and a tritium atom fuse to produce helium-4 (Figure 21.6.4), a process known as deuterium-tritium fusion (D–T fusion):
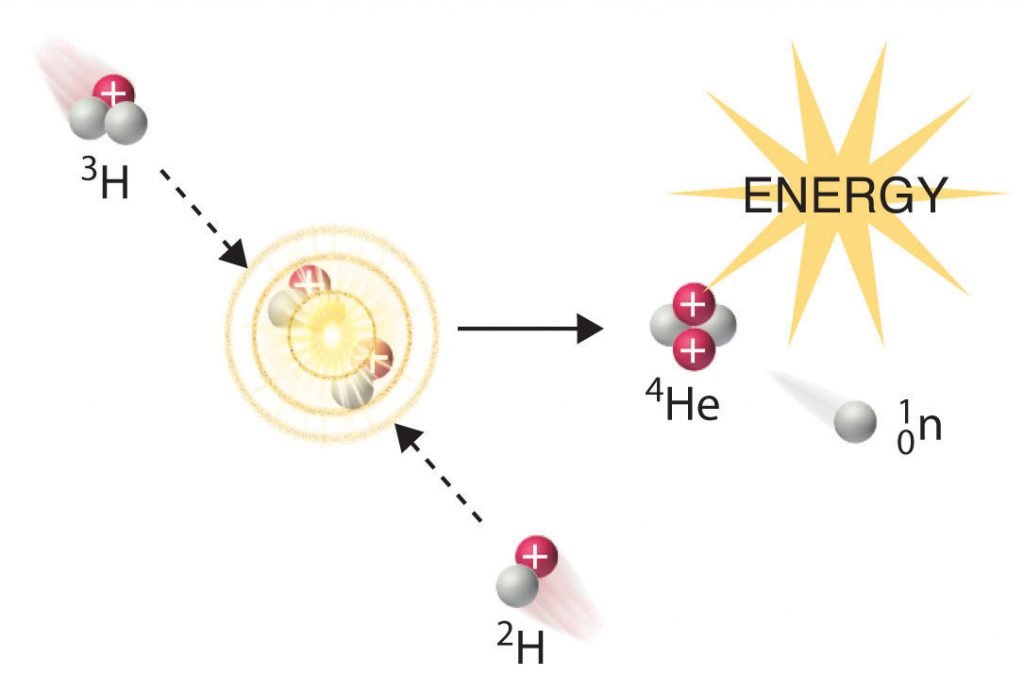
Figure 21.6.4 Nuclear Fusion. In a nuclear fusion reaction, lighter nuclei combine to produce a heavier nucleus. As shown, the fusion of 3H and 2H to give 4He and a neutron releases an enormous amount of energy. In principle, nuclear fusion can produce much more energy than fission, but very high kinetic energy is required to overcome electrostatic repulsions between the positively charged nuclei and initiate the fusion reaction.
Initiating these reactions, however, requires a temperature comparable to that in the interior of the sun (approximately 1.5 × 107 K). Currently, the only method available on Earth to achieve such a temperature is the detonation of a fission bomb. For example, the so-called hydrogen bomb (or H bomb) is a deuterium-tritium bomb (a D–T bomb), which uses a nuclear fission reaction to create the very high temperatures needed to initiate fusion of solid lithium deuteride (6LiD), which releases neutrons that then react with 6Li, producing tritium. The deuterium-tritium reaction releases energy explosively. Example 21.6.3 and its corresponding exercise demonstrate the enormous amounts of energy produced by nuclear fission and fusion reactions. Fusion reactions are the power sources for all-stars, including our sun.
To calculate the energy released during mass destruction in both nuclear fission and fusion, we use Einstein’s equation that equates energy and mass:
E=mc^2