Maxima and minima of a tabulated function

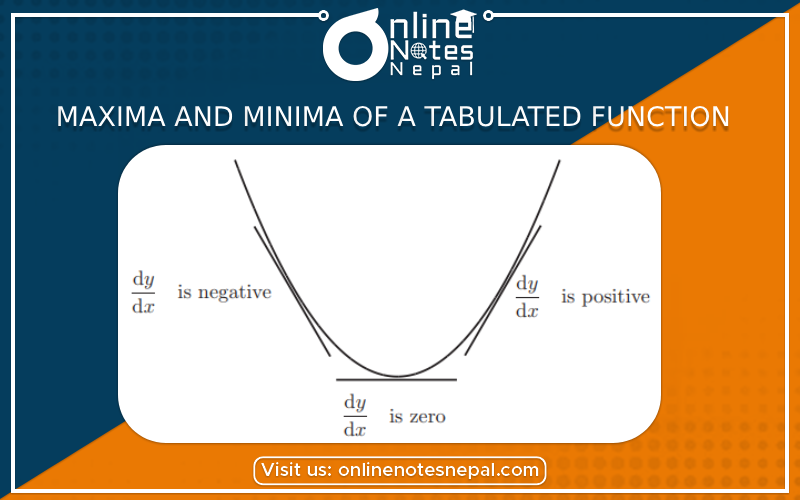
Finding the maxima and minima of a tabulated function involves identifying the highest (maximum) and lowest (minimum) values in the given table. A tabulated function is essentially a set of discrete data points where the function's values are provided for specific input values.

Here's a step-by-step process to find the maxima and minima of a tabulated function:

Step 1:

Examine the Table Look at the tabulated data and identify the input values (usually denoted as x) and the corresponding function values (usually denoted as f(x)).

Step 2:

Identify Maximum and Minimum Values Scan through the function values in the table to find the highest and lowest values. These highest and lowest function values represent the maxima and minima, respectively.

Step 3:

Determine Corresponding Input Values Note the input values (x) at which the maximum and minimum function values occur. These x-values correspond to the input values where the function reaches its highest and lowest points.

Step 4:

Interpret the Results Once you've found the maxima and minima, you can interpret the results in the context of the function's behavior. For example, the maximum value indicates the highest point on the function, and the minimum value represents the lowest point on the function within the range of the tabulated data. Keep in mind that finding maxima and minima from a table is an approximation since the data is discrete, and there may be peaks and valleys between the tabulated points that are not captured by the data. In cases where you need more accurate or continuous estimates of the maxima and minima, you can use interpolation techniques to estimate the function values at points between the tabulated data.

Additionally, for continuous functions represented by a mathematical expression, analytical methods like calculus can be used to find exact solutions for maxima and minima. These methods involve finding critical points (where the derivative of the function is zero or undefined) and using the second derivative test to determine whether these critical points correspond to maxima or minima. However, such analytical methods require a continuous representation of the function, which may not be available when dealing with tabulated data. In such cases, numerical methods or interpolation techniques can provide useful approximations for finding maxima and minima.