Matrix inversion and matrix factorization

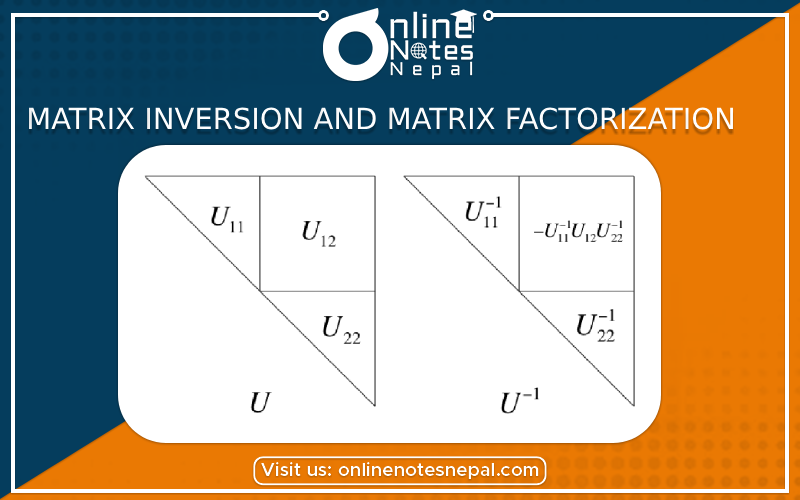
Matrix inversion and matrix factorization are fundamental concepts in linear algebra and play significant roles in various mathematical and computational applications.

Matrix Inversion:

Matrix inversion refers to the process of finding the inverse of a square matrix. Given a square matrix A, denoted as A^(-1), the inverse of A is a matrix such that when multiplied with A, it yields the identity matrix (I). The identity matrix is a square matrix with ones along the main diagonal and zeros elsewhere.

Mathematically, if A * A^(-1) = A^(-1) * A = I, then A^(-1) is the inverse of A. Not all matrices have inverses; those that do are called invertible or non-singular matrices. Matrices without inverses are called singular matrices.

The general formula to find the inverse of a 2x2 matrix (assuming it is invertible) is:

[ a  b ]
[ c  d ]

Inverse (A) = (1 / det(A)) * [ d  -b ]
                                          [ -c  a ]

Where det(A) is the determinant of matrix A, given by det(A) = ad - bc.

For larger matrices, the process becomes more involved, and various algorithms, such as Gaussian elimination, are used to find the inverse. Matrix inversion is often used in solving systems of linear equations, solving differential equations, and various numerical computations.

Matrix Factorization:

Matrix factorization involves representing a given matrix as a product of two or more matrices. The goal is to break down a complex matrix into simpler components, which can help in various applications such as data compression, solving systems of linear equations, and collaborative filtering in recommendation systems.

There are different types of matrix factorizations, each with its own purpose and properties. Some common matrix factorization techniques include:

• LU Factorization (Lower-Upper Factorization): Decomposes a matrix A into the product of a lower triangular matrix (L) and an upper triangular matrix (U).
• QR Factorization (QR Decomposition): Factorizes a matrix A into the product of an orthogonal matrix (Q) and an upper triangular matrix (R).
• Singular Value Decomposition (SVD): Decomposes a matrix A into the product of three matrices, where one is a diagonal matrix containing singular values.
• Eigenvalue Decomposition: Factorizes a matrix A into the product of its eigenvectors and eigenvalues.

Each of these factorizations has specific applications and properties, making them valuable tools in various mathematical and computational fields.

Matrix factorization is extensively used in numerical linear algebra, image and signal processing, machine learning (e.g., matrix completion and collaborative filtering), and many other areas where understanding the underlying structure of data is essential.