Published by: Sujan
Published date: 18 Jun 2021
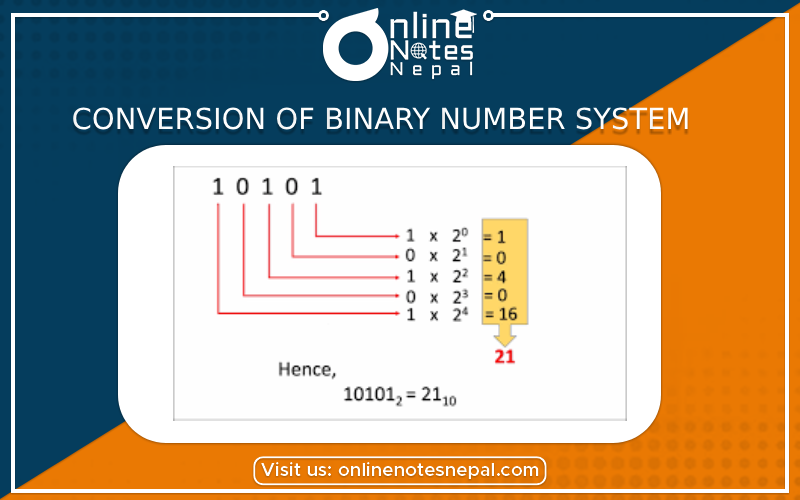
Conversion of Binary Number System can be studied in the following topics;
We know that the maximum digit in an octal number system is 7, which can be represented as 1112 in a binary system. Hence, starting from the LSB, we group three digits at a time and replace them by the decimal equivalent of those groups and we get the final octal number.
Example 1. Convert (101101010)2 into an equivalent octal number.
Solution. The binary number given is 101101010
Starting with LSB and grouping 3 bits 101 101 010
Octal equivalent 5 5 2
Hence the octal equivalent number is (552)8.
Example 2 Convert (1011110)2 into an equivalent octal number.
Solution. The binary number given is 1011110
Starting with LSB and grouping 3 bits 001 011 110
Octal equivalent 1 3 6
Hence the octal equivalent number is (136)8.
Since at the time of grouping the three digits in Example 1.14 starting from the LSB, we find that the third group cannot be completed, since only one 1 is left out in the third group, so we complete the group by adding two 0s in the MSB side. This is called the left padding of the number with 0. Now if the number has a fractional part then there will be two different classes of groups—one for the integer part starting from the left of the decimal point and proceeding toward the left and the second one starting from the right of the decimal point and proceeding toward the right. If, for the second class, and 1 is left out, we complete the group by adding two 0s on the right side. This is called right-padding.
Now if the octal number is given and you're asked to convert it into its binary equivalent, then each octal digit is converted into a 3-bit-equivalent binary number, and combining all those digits we get the final binary equivalent.
Example 3. Convert (235)8 into an equivalent binary number.
Solution. The octal number given is 2 3 5
3-bit binary equivalent 010 011 101
Hence the binary number is (010011101)2
Example 4. Convert (47.321)8 into an equivalent binary number.
Solution. The octal number given is 4 7 3 2 1
3-bit binary equivalent 100 111 011 010 001
Hence the binary number is (100111.011010001)2.
We know that the maximum digit in a hexadecimal system is 15, which can be represented by 11112 in a binary system. Hence, starting from the LSB, we group four digits at a time and replace them with the hexadecimal equivalent of those groups and we get the final hexadecimal number.
Example 1. Convert (11010110)2 into an equivalent hexadecimal number.
Solution. The binary number given is 11010110
Starting with LSB and grouping 4 bits 1101 0110
Hexadecimal equivalent D 6
Hence the hexadecimal equivalent number is (D6)16
Example 2. Convert (110011110)2 into an equivalent hexadecimal number.
Solution. The binary number given is 110011110
Starting with LSB and grouping 4 bits 0001 1001 1110
Hexadecimal equivalent 1 9 E
Hence the hexadecimal equivalent number is (19E)16.
Since at the time of grouping of four digits starting from the LSB, in Example 1.19 we find that the third group cannot be completed, since only one 1 is left out, so we complete the group by adding three 0s to the MSB side. Now if the number has a fractional part, as in the case of octal numbers, then there will be two different classes of groups—one for the integer part starting from the left of the decimal point and proceeding toward the left and the second one starting from the right of the decimal point and proceeding toward the right. If, for the second class, any uncompleted group is left out, we complete the group by adding 0s on the right side.
Example 3. Convert (111011.011)2 into an equivalent hexadecimal number.
Solution. The binary number given is 111011.011
Grouping 4 bits 0011 1011. 0110
Hexadecimal equivalent 3 B 6
Hence the hexadecimal equivalent number is (3B.6)16.
Now if the hexadecimal number is given and you're asked to convert it into its binary equivalent, then each hexadecimal digit is converted into a 4-bit-equivalent binary number and by combining all those digits we get the final binary equivalent.
Example 4. Convert (29C)16 into an equivalent binary number.
Solution. The hexadecimal number given is 2 9 C
4-bit binary equivalent 0010 1001 1100
Hence the equivalent binary number is (001010011100)2
Example 5. Convert (9E.AF2)16 into an equivalent binary number.
Solution. The hexadecimal number given is 9 E A F 2
4-bit binary equivalent 1001 1110 1010 1111 0010
Hence the equivalent binary number is (10011110.101011110010)2.